Phương pháp giải:

Thể tích khối cầu bán kính \(R\) là \(V=\dfrac{4}{3}\pi {{R}^{3}}\).

Lời giải chi tiết:

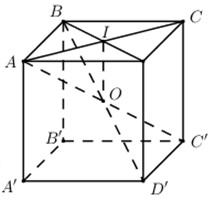
Gọi \(O\) là tâm hình lập phương \(ABCD.A'B'C'D'\). Gọi \(I\) là tâm hình vuông \(ABCD\).

Khi đó bán kính mặt cầu nội tiếp hình lập phương \(ABCD.A'B'C'D'\) là \(R=OI=\dfrac{a\sqrt{2}}{2}\).

Vậy thể tích khối cầu nội tiếp hình lập phương là:

\(V=\dfrac{4}{3}\pi {{R}^{3}}=\dfrac{4}{3}\pi {{\left( \dfrac{a\sqrt{2}}{2} \right)}^{3}}=\dfrac{\pi {{a}^{3}}\sqrt{2}}{3}\).

Chọn B.