Câu hỏi
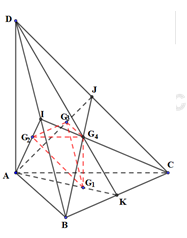
Cho tứ diện \(ABCD\)có các cạnh \(AB,AC\)và \(AD\) đôi một vuông góc với nhau. Gọi \({G_1},{G_2},{G_3}\)và \({G_4}\) lần lượt là trọng tâm các tam giác \(ABC,ABD,ACD\)và \(BCD\). Biết \(AB = 6a,\)\(AC = 9a\), \(AD = 12a\). Tính theo a thể tích khối tứ diện \({G_1}{G_2}{G_3}{G_4}\).
- A
\(4{a^3}\).
- B
\({a^3}\).
- C
\(108{a^3}\).
- D \(36{a^3}\).
Phương pháp giải:
Lập tỉ số thể tích của hai khối tứ diện là \({G_1}{G_2}{G_3}{G_4}\) và ABCD.
Lời giải chi tiết:
Gọi I, J, K lần lượt là trung điểm của BD, CD, BC.
Thể tích khối tứ diện vuông ABCD là: \(V = \dfrac{1}{6}.AB.AC.AD = \dfrac{1}{6}.6a.9a.12a = 108{a^3}\)
Ta có: \(\dfrac{{{G_2}{G_4}}}{{AC}} = \dfrac{{I{G_2}}}{{IA}} = \dfrac{{I{G_4}}}{{IC}} = \dfrac{1}{3}\), tương tự: \(\dfrac{{{G_2}{G_3}}}{{BC}} = \dfrac{{{G_3}{G_4}}}{{AB}} = \dfrac{{{G_1}{G_2}}}{{CD}} = \dfrac{{{G_1}{G_4}}}{{AD}} = \dfrac{{{G_1}{G_3}}}{{BD}} = \dfrac{1}{3}\)
\(\dfrac{{{V_{{G_1}{G_2}{G_3}{G_4}}}}}{{{V_{ABCD}}}} = {\left( {\dfrac{1}{3}} \right)^3} \Rightarrow {V_{{G_1}{G_2}{G_3}{G_4}}} = \dfrac{1}{{27}}.108{a^3} = 4{a^3}\).
Chọn: A
Câu hỏi trước
