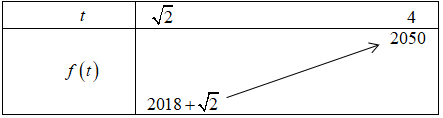Phương pháp giải:

Đặt \(t = \sqrt {2{x^2} + 3x + 2} \)  khi đó \(y = 2{t^2} + t + 2014 = f\left( t \right)\)

Lập bảng biến thiên để tìm giới hạn của \(t\) khi \(x \in \left[ {0;2} \right]\) từ đó lập bảng biến thiên  để tìm GTLN, GTNN của hàm số mới với biến \(t.\)

Lời giải chi tiết:

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 4{x^2} + \sqrt {2{x^2} + 3x + 2}  + 6x + 2018\) trên đoạn \(\left[ {0;2} \right]\)

Ta có hàm số:

\(y = 4{x^2} + \sqrt {2{x^2} + 3x + 2}  + 6x + 2018 = 2\left( {2{x^2} + 3x + 2} \right) + \sqrt {2{x^2} + 3x + 2}  + 2014.\)

Đặt \(t = \sqrt {2{x^2} + 3x + 2} \;\;\;\left( {t \ge 0} \right) \Rightarrow {t^2} = 2{x^2} + 3x + 2.\)  

Khi đó ta có hàm số: \(y = f\left( t \right) = 2{t^2} + t + 2014.\)

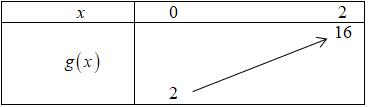
Xét \(g\left( x \right) = 2{x^2} + 3x + 2\) với \(x \in \left[ {0;2} \right]\)

Ta có bảng:

\( \Rightarrow \) Với \(x \in \left[ {0;2} \right]\) thì \(g\left( x \right) \in \left[ {2;16} \right]\)

\( \Rightarrow t = \sqrt {2{x^2} + 3x + 2}  = \sqrt {g\left( x \right)}  \in \left[ {\sqrt 2 ;4} \right]\)

Bài toán trở thành tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( t \right) = 2{t^2} + t + 2014\) trên đoạn \(\left[ {\sqrt 2 ;4} \right].\)

Ta có bảng:

Vậy GTNN của hàm số bằng \(2018 + \sqrt 2 \) đạt được khi \(t = \sqrt 2 \) hay \(x = 0.\)

Vậy GTLN của hàm số bằng \(2050\) đạt được khi \(t = 4\) hay \(x = 2.\)

Chọn A.