Phương pháp giải:

- Bán kính của mặt cầu (S) bằng khoảng cách từ I đến \(\Delta \) (do (S) tiếp xúc với đường thẳng \(\Delta \))

- Công thức khoảng cách từ điểm đến đường thẳng trong không gian: \(d\left( {A;\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow u ;\overrightarrow {MA} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) , với \(\overrightarrow u \) là VTCP của \(\Delta \) và M là điểm bất kì thuộc \(\Delta \).

Lời giải chi tiết:

Do (S) tiếp xúc với đường thẳng \(\Delta \) nên bán kính của mặt cầu (S) bằng khoảng cách từ I đến \(\Delta \)

Lấy \(M\left( { - 2;1;0} \right) \in \Delta  \Rightarrow \overrightarrow {MI}  = \left( {4;0; - 1} \right)\)

\(\Delta \) có 1 VTCP là: \(\overrightarrow u  = \left( {2;2; - 1} \right) \Rightarrow \left[ {\overrightarrow u ;\overrightarrow {MI} } \right] = \left( { - 2; - 2; - 8} \right)\)

\(d\left( {I;\Delta } \right) = \dfrac{{\left| {\left[ {\overrightarrow u ;\overrightarrow {MI} } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \dfrac{{\left| {4 + 4 + 64} \right|}}{{\left| {4 + 4 + 1} \right|}} = 2\sqrt 2  \Rightarrow R = 2\sqrt 2  \Rightarrow IA = IB = 2\sqrt 2 \)

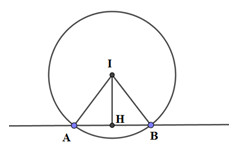
\(d\left( {I;Ox} \right) = 2 = IH\)

Ta có : \(AH = \sqrt {I{A^2} - I{H^2}}  = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {2^2}}  = 2\,\, \Rightarrow AB = 4\).

Chọn: C