Câu hỏi
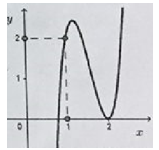
Cho hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\) có bao nhiêu đường tiệm cận đứng?
- A 5
- B 2
- C 3
- D 6
Phương pháp giải:
* Định nghĩa tiệm cận đứng của đồ thị hàm số \(y = f(x)\).
Nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ + }} f(x) = - \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = + \infty \,\)hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f(x) = - \infty \,\)thì \(x = a\) là TCĐ của đồ thị hàm số.
Lời giải chi tiết:
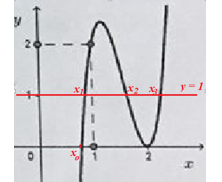
\(f\left( 1 \right) = 2,\,\,f\left( {x{ & _0}} \right) = f\left( 2 \right) = 0,\,\,f\left( {{x_1}} \right) = f\left( {{x_2}} \right) = f\left( {{x_3}} \right) = 1\)
Xét hàm số \(g\left( x \right) = \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\), có ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 1\\x \ne 0\\f\left( x \right) \ne 0\\f\left( x \right) \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne 0\\x \ne {x_0}\\x \ne {x_1}\\x \ne {x_2}\\x \ne {x_3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\x \ne {x_2}\\x \ne {x_3}\end{array} \right.,\,\,\,\,1 < {x_2} < 2 < {x_3}\)
\(\mathop {\lim }\limits_{x \to {x_2}} g(x) = \mathop {\lim }\limits_{x \to {x_2}} \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \infty \),\(\mathop {\lim }\limits_{x \to {x_3}} g(x) = \mathop {\lim }\limits_{x \to {x_3}} \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \infty \)
\( \Rightarrow \)đồ thị hàm số \(g\left( x \right) = \dfrac{{\left( {{x^2} - 4x + 4} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}}\) có 2 đường tiệm cận đứng.
Chọn: B