Câu hỏi
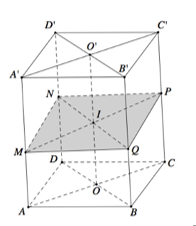
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng 1. Gọi M là điểm thỏa mãn \(\overrightarrow {BM} = \dfrac{2}{3}\overrightarrow {BB'} \) và N là trung điểm của DD’. Mặt phẳng (AMN) chia hình hộp thành hai phần, thể tích phần có chứa điểm A’ bằng
- A \(\dfrac{{67}}{{144}}\).
- B \(\dfrac{4}{9}\).
- C \(\dfrac{3}{8}\)
- D \(\dfrac{{181}}{{432}}\).
Phương pháp giải:
\(\dfrac{{AM}}{{AA'}} = x,\,\dfrac{{BN}}{{BB'}} = y,\,\,\dfrac{{CP}}{{CC'}} = z,\,\,\dfrac{{DQ}}{{DD'}} = t \Rightarrow \left\{ \begin{array}{l}x + z = y + t\\\dfrac{{{V_{ABCD.MNPQ}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{{x + y + z + t}}{4}\end{array} \right.\)
Lời giải chi tiết:
Gọi O, O’ lần lượt là tâm của các hình bình hành ABCD, A’B’C’D’.
Trong (BDD’B’), gọi I là giao điểm của OO’ và MN
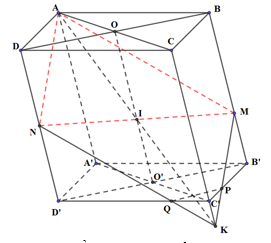
Trong (ACC’A’), gọi K là giao điểm của AI và CC’
Trong (CDD’C’), gọi Q là giao điểm của NK và C’D’
Trong (CBB’C’), gọi P là giao điểm của MK và C’B’
\( \Rightarrow \)Thiết diện của hình hộp cắt bởi mặt phẳng (AMN) là ngũ giác AMPQN.
Đặt \(\dfrac{{AA'}}{{AA'}} = x = 0,\,\dfrac{{BM}}{{BB'}} = y = \dfrac{2}{3},\,\,\dfrac{{CK}}{{CC'}} = z,\,\,\dfrac{{DN}}{{DD'}} = t = \dfrac{1}{2} \Rightarrow \left\{ \begin{array}{l}x + z = y + t\\\dfrac{{{V_{ABCD.AMKN}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{{x + y + z + t}}{4}\end{array} \right.\)
\(0 + z = \dfrac{1}{2} + \dfrac{2}{3} \Rightarrow z = \dfrac{7}{6}\)
\(\dfrac{{{V_{ABCD.AMKN}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{{x + y + z + t}}{4} = \dfrac{{0 + \dfrac{2}{3} + \dfrac{7}{6} + \dfrac{1}{2}}}{4} = \dfrac{{\dfrac{7}{3}}}{4} = \dfrac{7}{{12}} \Rightarrow {V_{ABCD.AMKN}} = \dfrac{7}{{12}}{V_{ABCD.A'B'C'D'}} = \dfrac{7}{{12}}.1 = \dfrac{7}{{12}}\) (1)
\({V_{K.CQP}} = \dfrac{1}{3}.{d_{\left( {K;\left( {A'B'C'D'} \right)} \right)}}.{S_{\Delta CQP}}\)
Mà \({d_{\left( {K;\left( {A'B'C'D'} \right)} \right)}} = \dfrac{1}{6}{d_{\left( {C;\left( {A'B'C'D'} \right)} \right)}}\) (do \(z = \dfrac{{CK}}{{CC'}} = \dfrac{7}{6}\)) và \({S_{\Delta CQP}} = \dfrac{1}{4}.\dfrac{1}{3}{S_{\Delta C'B'D'}} = \dfrac{1}{{24}}{S_{A'B'C'D'}}\)
(do \(\dfrac{{CQ}}{{D'Q}} = \dfrac{{C'K}}{{ND'}} = \dfrac{{\dfrac{1}{6}}}{{\dfrac{1}{2}}} = \dfrac{1}{3} \Rightarrow \dfrac{{C'Q}}{{C'D'}} = \dfrac{1}{4}\); \(\dfrac{{C'P}}{{PB'}} = \dfrac{{C'K}}{{MB'}} = \dfrac{{\dfrac{1}{6}}}{{\dfrac{1}{3}}} = \dfrac{1}{2} \Rightarrow \dfrac{{C'P}}{{B'C'}} = \dfrac{1}{3}\))
\( \Rightarrow {V_{K.CQP}} = \dfrac{1}{3}.\dfrac{1}{6}{d_{\left( {C';\left( {A'B'C'D'} \right)} \right)}}.\dfrac{1}{{24}}{S_{A'B'C'D'}} = \dfrac{1}{{432}}{d_{\left( {C';\left( {A'B'C'D'} \right)} \right)}}.{S_{A'B'C'D'}} = \dfrac{1}{{432}}.{V_{ABCD.A'B'C'D'}} = \dfrac{1}{{432}}\) (2)
Từ (1), (2) suy ra: \({V_{ABCD.MPCQN}} = \dfrac{7}{{12}} - \dfrac{1}{{432}} = \dfrac{{251}}{{432}}\)
\( \Rightarrow \) Thể tích cần tìm là: \(1 - \dfrac{{251}}{{432}} = \dfrac{{181}}{{432}}\).
Chọn: D