Câu hỏi
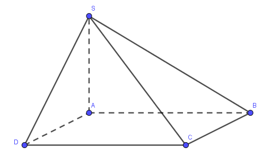
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, \(BC = a\sqrt 3 \). Cạnh bên SA vuông góc với đáy và đường thẳng SD tạo với mặt phẳng (ABCD) một góc \({30^0}\). Thể tích của khối chóp S.ABCD bằng:
- A \(\dfrac{{\sqrt 3 {a^3}}}{3}\).
- B \(\dfrac{{2{a^3}}}{3}\).
- C \(\sqrt 3 {a^3}\).
- D \(\dfrac{{2\sqrt 6 {a^3}}}{3}\).
Phương pháp giải:
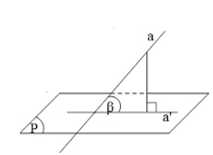
+) Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
+) Thể tích khối chóp có diện tích đáy S và chiều cao h là \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết:
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat {\left( {SD;\left( {ABCD} \right)} \right)} = \widehat {SDA} = {30^0}\)
\(\Delta SAD\) vuông tại A\( \Rightarrow SA = AD.\tan \widehat {SDA} = a\sqrt 3 .\tan {30^0} = a\)
Diện tích hình chữ nhật ABCD: \({S_{ABCD}} = a.a\sqrt 3 = {a^2}\sqrt 3 \).
Thể tích của khối chóp S.ABCD là: \(V = \dfrac{1}{3}{S_{ABCD}}.SA = \dfrac{1}{3}.{a^2}\sqrt 3 .a = \dfrac{{\sqrt 3 }}{3}{a^3}\).
Chọn: A