Câu hỏi
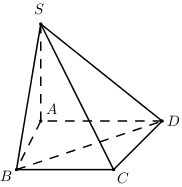
Cho hình chóp \(S.ABCD\) có đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) , đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B\) , có \(AB = a,\,AD = 2a,BC = a.\) Biết rằng \(SA = a\sqrt 2 .\) Tính thể tích \(V\) của khối chóp \(S.ABCD\) theo \(a.\)
- A \(V = \frac{{{a^3}\sqrt 2 }}{2}\)
- B \(V = \frac{{2{a^3}\sqrt 2 }}{3}\)
- C \(V = 2{a^3}\sqrt 2 \)
- D \(V = \frac{{{a^3}\sqrt 2 }}{6}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp \(V = \frac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
Ta có \({S_{ABCD}} = \frac{{\left( {AD + BC} \right).AB}}{2} = \frac{{\left( {2a + a} \right).a}}{2} = \frac{{3{a^2}}}{2}\) ; \({S_{ABD}} = \frac{1}{2}AB.AD = \frac{1}{2}.a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \frac{3}{2}{a^2} - {a^2} = \frac{{{a^2}}}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.a\sqrt 2 .\frac{{{a^2}}}{2} = \frac{{{a^3}\sqrt 2 }}{6}\).
Chọn D.
Câu hỏi trước
