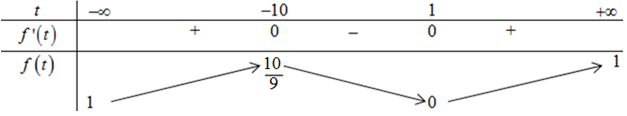Phương pháp giải:

+) Lấy y chia y’, phần dư chính là phương trình tiếp tuyến đi qua 2 điểm cực trị của hàm số.

+) Sử dụng công thức tính khoảng cách từ 1 điểm \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\left( d \right):\,\,ax + by + c = 0\) là \(d\left( {M;d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\).

+) Xét hàm số và tìm GTLN của hàm số bằng cách lập BBT.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\). Ta có \(y' = {x^2} - 4mx + m - 1\).

Lấy \(y\) chia cho \(y'\)  ta được \(y = y'\left( {\frac{1}{3}x - \frac{2}{3}m} \right) + \left( { - \frac{8}{3}{m^2} + \frac{2}{3}m - \frac{2}{3}} \right)x + \frac{8}{3}{m^2} - \frac{2}{3}m + 1\)

\( \Rightarrow \) Phương trình đường thẳng đi qua 2 điểm cực trị của hàm số là \(y = \left( { - \frac{8}{3}{m^2} + \frac{2}{3}m - \frac{2}{3}} \right)x + \frac{8}{3}{m^2} - \frac{2}{3}m + 1\).

\(\begin{array}{l} \Leftrightarrow \left( { - \frac{8}{3}{m^2} + \frac{2}{3}m - \frac{2}{3}} \right)x - y + \frac{8}{3}{m^2} - \frac{2}{3}m + 1 = 0\\ \Leftrightarrow \left( { - 8{m^2} + 2m - 2} \right)x - 3y + 8{m^2} - 2m + 3 = 0\,\,\left( d \right)\\ \Rightarrow d\left( {O;d} \right) = \frac{{\left| {8{m^2} - 2m + 3} \right|}}{{\sqrt {{{\left( { - 8{m^2} + 2m - 2} \right)}^2} + 9} }} = \sqrt {\frac{{{{\left( {8{m^2} - 2m + 3} \right)}^2}}}{{{{\left( { - 8{m^2} + 2m - 2} \right)}^2} + 9}}} \end{array}\)

Đặt \(t =  - 8{m^2} + 2m - 2 \Rightarrow  - t + 1 = 8{m^2} - 2m + 3\)

\( \Rightarrow d\left( {O;d} \right) = \sqrt {\frac{{{{\left( { - t + 1} \right)}^2}}}{{{t^2} + 9}}} \).

Xét hàm số \(f\left( t \right) = \frac{{{{\left( { - t + 1} \right)}^2}}}{{{t^2} + 9}}\) ta có \(f'\left( t \right) = \frac{{ - 2\left( { - t + 1} \right)\left( {{t^2} + 9} \right) - {{\left( { - t + 1} \right)}^2}.2t}}{{{{\left( {{t^2} + 10} \right)}^2}}} = \frac{{2{t^2} + 16t - 18}}{{{{\left( {{t^2} + 10} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - 9\end{array} \right.\).

BBT:

\( \Rightarrow d{\left( {O;d} \right)_{\max }} = \frac{{\sqrt {10} }}{3}\) .

Chọn D.