Câu hỏi
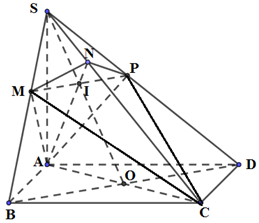
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(2\sqrt 2 \), cạnh bên SA vuông góc với mặt đáy. Mặt phẳng \(\left( \alpha \right)\) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
- A \(V = \frac{{108\pi }}{3}\).
- B \(V = \frac{{64\sqrt 2 \pi }}{3}\).
- C \(V = \frac{{125\pi }}{6}\).
- D \(V = \frac{{32\pi }}{3}\).
Phương pháp giải:
+ Chứng minh: O là tâm mặt cầu ngoại tiếp tứ diện CMNP (với O là tâm của hình vuông ABCD)
+ Thể tích khối cầu có bán kính \(r\) là: \(V = \frac{4}{3}\pi {r^3}\).
Lời giải chi tiết:
Gọi O là tâm của hình vuông ABCD \( \Rightarrow O\) là trung điểm của AC
Ta có: \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAD} \right) \Rightarrow CD \bot AP\)
\(\left\{ \begin{array}{l}SC \bot AP\,\,\left( {do\,\,SC \bot \left( \alpha \right)} \right)\\CD \bot AP\end{array} \right. \Rightarrow AP \bot \left( {SCD} \right) \Rightarrow AP \bot CP \Rightarrow \Delta APC\) vuông tại P \( \Rightarrow OA = OC = OP\)
Tương tự, ta có: \(\Delta AMC\) vuông tại M \( \Rightarrow OA = OC = OM\)
Lại có: \(SC \bot AN\,\,\,\left( {do\,\,SC \bot \left( \alpha \right)} \right) \Rightarrow \Delta ANC\) vuông tại N \( \Rightarrow OA = OC = ON\)
\( \Rightarrow OA = OC = OP = OM = ON \Rightarrow \) O là tâm mặt cầu ngoại tiếp tứ diện CMNP
Bán kính : \(R = OA = \frac{{AB}}{{\sqrt 2 }} = \frac{{2\sqrt 2 }}{{\sqrt 2 }} = 2\)
Thể tích khối cầu ngoại tiếp tứ diện CMNP là: \(V = \frac{4}{3}\pi {.2^3} = \frac{{32\pi }}{3}\).
Chọn: D