Câu hỏi
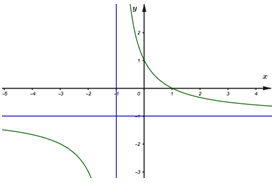
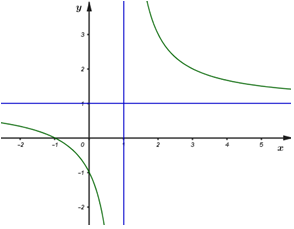
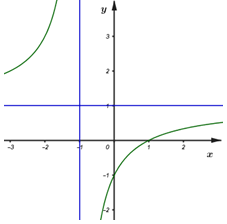
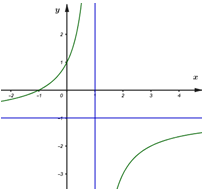
Đồ thị hàm số \(y = \frac{{x + 1}}{{1 - x}}\) có dạng:
- A
- B
- C
- D
Phương pháp giải:
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}},\left( {ad - bc \ne 0,\,\,c \ne 0} \right)\) có TCĐ: \(x = \frac{{ - d}}{c}\) và TCN: \(y = \frac{a}{c}\)
Nếu \(ad - bc > 0\) thì hàm số đồng biến trên từng khoảng xác định
Nếu \(ad - bc < 0\) thì hàm số nghịch biến trên từng khoảng xác định.
Lời giải chi tiết:
Đồ thị hàm số \(y = \frac{{x + 1}}{{1 - x}}\) có TCĐ: \(x = 1\) và TCN: \(y = - 1\) và đồng biến trên từng khoảng xác định do \(1.1 - 1.\left( { - 1} \right) = 2 > 0\)
\( \Rightarrow \)Chọn đồ thị ở câu D
Chọn: D