Phương pháp giải:

Ta xác định tâm mặt cầu ngoại tiếp tứ diện \(ABCD\) chính là điểm cách đều bốn đỉnh \(A,B,C,D.\)

Dựa vào tính chất tam giác cân, hai tam giác bằng nhau, tỉ số lượng giác để chứng minh các đoạn thẳng bằng nhau từ đó tìm được tâm mặt cầu.

Lời giải chi tiết:

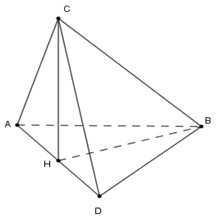
Các tam giác đều \(ABC\) và \(BCD\) có cạnh 2

\( \Rightarrow BD = DC = BC = AB = AC = 2\)

Nên tam giác \(CAD\) cân tại \(C\) và  tam giác \(BAD\) cân tại \(B.\)

Lấy \(H\) là trung điểm \(AD \Rightarrow CH \bot AD\) (do tam giác \(CAD\) cân tại \(C\))

Ta có \(\left\{ \begin{array}{l}\left( {CAD} \right) \bot \left( {BAD} \right)\\\left( {CAD} \right) \cap \left( {BAD} \right) = AD\\CH \bot AD,\,CH \subset \left( {CAD} \right)\end{array} \right. \Rightarrow CH \bot \left( {BAD} \right) \Rightarrow CH \bot BH\)  (1)

Lại có  \(\Delta CAD = \Delta BAD\left( {c - c - c} \right)\) nên \(BH = CH\) (2)

Từ (1) và (2) suy ra tam giác \(CHB\) vuông cân tại \(H\) có cạnh huyền \(CB = 2.\).

Suy ra \(B{C^2} = B{H^2} + C{H^2} \Leftrightarrow 2B{H^2} = {2^2} \Rightarrow BH = CH = \sqrt 2 .\)

Xét tam giác \(CAH\) vuông tại \(H\) có \(\cos \widehat {ACH} = \dfrac{{CH}}{{AC}} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \widehat {ACH} = 45^\circ \)

Lại thấy \(CH\) là phân giác của \(\widehat {ACD}\)  (vì \(\Delta CAD\) cân tại \(C\)) nên \(\widehat {ACH} = \widehat {HCD} = 45^\circ  \Rightarrow \widehat {ACD} = 90^\circ \)

Hay tam giác \(CAD\) vuông cân tại \(C \Rightarrow CH = \dfrac{1}{2}AD = HA = HD\) (3)

Vì \(\Delta CAD = \Delta BAD\left( {c - c - c} \right)\) nên \(\Delta ABD\) vuông cân tại \(B \Rightarrow BH = \dfrac{{AD}}{2} = HD = HA\) (4)

Từ (3) và (4) suy ra \(HA = HB = HC = HD = \sqrt 2 \)  hay \(H\) là tâm mặt cầu ngoại tiếp tứ diện \(ABCD\) và bán kính mặt cầu là \(\sqrt 2 \).

Chọn B.