Phương pháp giải:

Xác định tâm mặt cầu ngoại tiếp hình chóp đều là giao của đường trung trực 1 cạnh bên và chiều cao của hình chóp.

Từ đó sử dụng tam giác đồng dạng để tính bán kính mặt cầu ngoại tiếp hình chóp đều.

Lời giải chi tiết:

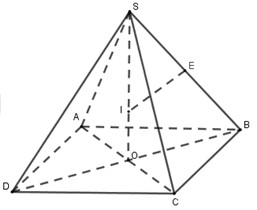
Gọi \(O\) là tâm hình vuông \(ABCD\) và \(E\) là trung điểm \(SB.\)

Vì \(S.ABCD\) là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\)

Trong \(\left( {SBO} \right)\) kẻ đường trung trực của \(SB\) cắt \(SO\) tại \(I\), khi đó \(IA = IB = IC = ID = IS\)  nên \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) và bán kính mặt cầu là \(R = IS.\)

Ta có \(ABCD\) là hình vuông cạnh \(2\)

 \( \Rightarrow BD = \sqrt {B{C^2} + C{D^2}}  = 2\sqrt 2  \Rightarrow BO = \dfrac{{BD}}{2} = \sqrt 2 .\)

Ta có \(SA = SB = SC = SD = 3\sqrt 2 \) (vì \(S.ABCD\) là hình chóp đều) nên \(SE = EB = \dfrac{{3\sqrt 2 }}{2}\)

Xét tam giác \(SBO\) vuông tại \(O\) (vì \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OB\)) có \(SO = \sqrt {S{B^2} - O{B^2}}  = \sqrt {18 - 2}  = 4.\)

Ta có \(\Delta SEI\) đồng dạng với tam giác \(SOB\left( {g - g} \right) \Rightarrow \dfrac{{SI}}{{SB}} = \dfrac{{SE}}{{SO}} \Leftrightarrow IS = \dfrac{{SB.SE}}{{SO}} = \dfrac{{3\sqrt 2 .\dfrac{{3\sqrt 2 }}{2}}}{4} = \dfrac{9}{4}\)

Vậy bán kính \(R = \dfrac{9}{4}.\)

Chọn C.