Phương pháp giải:

Thể tích khối nón có bán kính đáy \(r\), chiều cao \(h\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

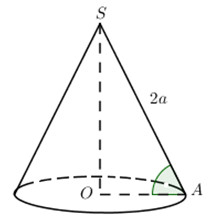
Giả sử hình nón có đỉnh \(S\) và \(O\) là tâm đường tròn đáy. Lấy \(A\) là điểm bất kì trên đường tròn đáy ta có \(\angle SAO = {60^0}\).

Xét tam giác vuông \(SAO\) ta có:

\(\begin{array}{l}SO = SA.\sin {60^0} = 2a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3  = h\\OA = SA.\cos {60^0} = 2a.\dfrac{1}{2} = a = r\end{array}\)

Vậy thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {a^2}.a\sqrt 3  = \dfrac{{\pi {a^3}\sqrt 3 }}{3}\).

Chọn B.