Câu hỏi
Một khối gỗ hình lập phương có thể tích \({V_1}\). Một người thợ mộc muốn gọt giũa khối gỗ đó thành một khối trụ có thể tích là \({V_2}\). Tính tỉ số lớn nhất \(k = \dfrac{{{V_2}}}{{{V_1}}}\)?
- A \(k = \dfrac{\pi }{4}\)
- B \(k = \dfrac{2}{\pi }\)
- C \(k = \dfrac{\pi }{2}\)
- D \(k = \dfrac{4}{\pi }\)
Phương pháp giải:
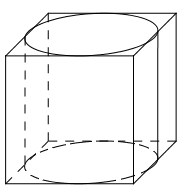
Tỉ số \(\dfrac{{{V_2}}}{{{V_1}}}\) lớn nhất khi và chỉ khi \({V_2}\) lớn nhất. Khi đó hình trụ có chiều cao bằng cạnh của hình lập phương và có đường tròn đáy nội tiếp một mặt của hình lập phương.
Lời giải chi tiết:
Gọi \(a\) là cạnh của hình lập phương, khi đó thể tích của hình lập phương là \({V_1} = {a^3}\). Khi đó tỉ số \(\dfrac{{{V_2}}}{{{V_1}}}\) lớn nhất khi và chỉ khi \({V_2}\) lớn nhất.
Khi đó hình trụ có chiều cao bằng cạnh của hình lập phương và có đường tròn đáy nội tiếp một mặt của hình lập phương.
\( \Rightarrow h = a,\,\,r = \dfrac{a}{2}\).
Khi đó \({V_2} = \pi {r^2}h = \pi {\left( {\dfrac{a}{2}} \right)^2}.a = \dfrac{{\pi {a^3}}}{4}\)
Vậy \(k = \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{\pi }{4}\).
Chọn A.