Câu hỏi
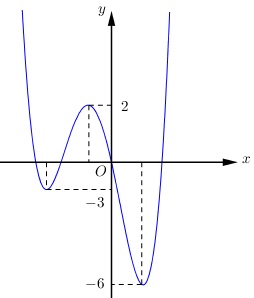
Hình vẽ bên là đồ thị cảu hàm số \(y = f\left( x \right)\) Gọi \(S\) là tập hợp các giá trị nguyên không âm của tham số \(m\) để hàm số \(y = \left| {f\left( {x - 2019} \right) + m - 2} \right|\) có 5 điểm cực trị. Số các phần tử của \(S\) bằng
- A \(3\)
- B \(4\)
- C \(2\)
- D \(5\)
Phương pháp giải:
+) Xác định cách vẽ đồ thị hàm số \(y = \left| {f\left( {x - 2019} \right) + m - 2} \right|\).
+) Hàm số \(y = \left| {f\left( {x - 2019} \right) + m - 2} \right|\) với \(f\left( {x - 2019} \right) + m - 2\) là đa thức bậc bốn có 5 cực trị khi và chỉ khi đồ thị hàm số \(y = f\left( {x - 2019} \right) + m - 2\) có \({y_{CD}}.{y_{CT}} \le 0\).
Lời giải chi tiết:
Đồ thị hàm số \(y = f\left( {x - 2019} \right)\) được tạo thành bằng cách tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) theo chiều song song với trục Ox sang bên phải 2019 đơn vị.
Đồ thị hàm số \(y = f\left( {x - 2019} \right) + m - 2\) được tạo thành bằng cách tịnh tiến đồ thị hàm số \(f\left( {x - 2019} \right)\) theo chiều song song với trục Oy lên trên \(m - 2\) đơn vị.
Đồ thị hàm số \(y = \left| {f\left( {x - 2019} \right) + m - 2} \right|\) được tạo thành bằng giữ nguyên phần đồ thị \(y = f\left( {x - 2019} \right) + m - 2\) phía trên trục Ox, lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua trục Ox và xóa đi phần đồ thị phía dưới trục Ox.
Do đó để đồ thị hàm số \(y = \left| {f\left( {x - 2019} \right) + m - 2} \right|\) có 5 điểm cực trị thì đồ thị hàm số \(y = f\left( {x - 2019} \right) + m - 2\) có \({y_{CD}}.{y_{CT}} \le 0\).
\( \Leftrightarrow - 3 + m - 2 \ge 0 > - 6 + m - 2 \Leftrightarrow m - 5 \ge 0 > m - 8 \Leftrightarrow 5 \le m < 8\)
\( \Rightarrow \) có 3 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.
Chọn A.







