Câu hỏi
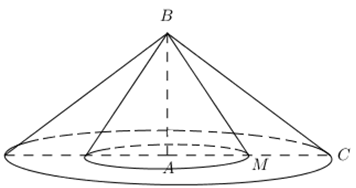
Cho tam giác \(ABC\) vuông tại \(A\) , cạnh \(AB = 6,AC = 8\) và \(M\) là trung điểm của cạnh Khi đó thể tích của khối tròn xoay do tam giác quanh cạnh là
- A \(86\pi \)
- B \(106\pi \)
- C \(96\pi \)
- D \(98\pi \)
Phương pháp giải:
Sử dụng công thức tính thể tích khối nón có chiều cao \(h\) và bán kính đáy \(r\) là \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
Khi quay tam giác \(BMC\) quanh cạnh \(AB\) tạo ra 2 khối tròn xoay có thể tích là:
\(V = \frac{1}{3}\pi .A{C^2}.AB - \frac{1}{3}\pi A{M^2}AB = \frac{1}{3}\pi {.8^2}.6 - \frac{1}{3}\pi {.4^2}.6 = 96\pi \).
Chọn C.
Câu hỏi trước
