Phương pháp giải:

+) Gọi \(D\) là trung điểm của \(BC\), \(H = MN \cap SD\). Chứng minh \(SH \bot \left( {AMN} \right)\).

+) Chứng minh \(\Delta AMN\) cân tại \(A \Rightarrow {S_{\Delta AMN}}\).

+) Tính \({V_{S.AMN}} = \frac{1}{3}SH.{S_{\Delta AMN}}\).

+) Sử dụng công thức tỉ lệ thể tích Simpson, tính \({V_{S.ABC}}\).

Lời giải chi tiết:

Gọi \(D\) là trung điểm của \(BC\). Do \(\Delta SBC\) cân tại \(S \Rightarrow SD \bot BC\).

\(MN\) là đường trung bình của \(\Delta SBC \Rightarrow MN//BC \Rightarrow MN \bot SD\) và \(MN = \frac{1}{2}BD = \frac{a}{2}\).

Gọi \(H = MN \cap SD \Rightarrow SH \bot MN\)

Ta có : \(\left\{ \begin{array}{l}\left( {AMN} \right) \bot \left( {SCD} \right)\\\left( {AMN} \right) \cap \left( {SCD} \right) = MN\\\left( {SCD} \right) \supset SH \bot MN\end{array} \right. \Rightarrow SH \bot \left( {AMN} \right)\).

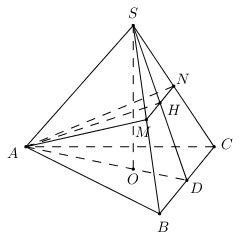
Tương tự ta chứng minh được \(AH \bot \left( {SCD} \right) \Rightarrow AH \bot SD\) tại \(H\) là trung điểm của \(SD\).

\( \Rightarrow \Delta SAD\) cân tại \(A \Rightarrow SA = AD = \frac{{a\sqrt 3 }}{2} = SB = SC\).

Áp dụng định lí Pytago trong tam giác vuông \(SBD\) có \(SD = \sqrt {S{B^2} - B{D^2}}  = \frac{{a\sqrt 2 }}{2}\).

\( \Rightarrow SH = \frac{1}{2}SD = \frac{{a\sqrt 2 }}{4}\).

Áp dụng định lí Pytago trong tam giác vuông \(SAH\) ta có \(AH = \sqrt {S{A^2} - S{H^2}}  = \frac{{a\sqrt {10} }}{4}\).

\( \Rightarrow {S_{\Delta AMN}} = \frac{1}{2}AH.MN = \frac{1}{2}\frac{{a\sqrt {10} }}{4}.\frac{a}{2} = \frac{{{a^2}\sqrt {10} }}{{16}}\)

\( \Rightarrow {V_{S.AMN}} = \frac{1}{3}SH.{S_{\Delta AMN}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{4}.\frac{{{a^2}\sqrt {10} }}{{16}} = \frac{{{a^2}\sqrt 5 }}{{96}}\)

Ta có: \(\frac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = \frac{1}{4} \Rightarrow {V_{S.ABC}} = 4{V_{S.AMN}} = \frac{{{a^3}\sqrt 5 }}{{24}}\).

Chọn B.