Phương pháp giải:

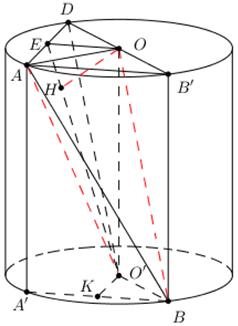
+) Dựng \(AA'//OO',\,\,BB''//OO'\) (A’ thuộc đường tròn \(\left( {O'} \right)\) và \(B'\) thuộc đường tròn \(\left( O \right)\))

+) Xác định khoảng cách giữa OO’ và AB, chứng minh tam giác OAB’ vuông cân tại O.

+) Xác định mặt phẳng chưa O’A và song song với OB, đưa về bài toán khoảng cách từ điểm đếm mặt phẳng.

+) Xác định khoảng cách, áp dụng hệ thức lượng trong tam giác vuông tính khoảng cách.

Lời giải chi tiết:

Dựng \(AA'//OO',\,\,BB''//OO'\) (A’ thuộc đường tròn \(\left( {O'} \right)\) và \(B'\) thuộc đường tròn \(\left( O \right)\))

Ta có:

\(\begin{array}{l}OO'//\left( {AA'B} \right) \supset AB\\ \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {AA'B} \right)} \right) = d\left( {O';\left( {AA'B} \right)} \right)\end{array}\)

Gọi \(K\) là trung điểm của \(A'B\) ta có

\(\left\{ \begin{array}{l}O'K \bot A'B\\O'K \bot AA'\end{array} \right. \Rightarrow O'K \bot \left( {AA'B} \right) \Rightarrow d\left( {OO';\left( {AA'B} \right)} \right) = O'K = 2\sqrt 2 \)

Xét tam giác vuông \(O'KB\) có :

\(\cos \angle O'BK = \frac{{O'K}}{{O'B}} = \frac{{2\sqrt 2 }}{4} = \frac{{\sqrt 2 }}{2} \Rightarrow \angle O'BK = {45^0}\).

\(\Delta O'A'B\) cân tại \(O'\) có \(\angle O'BA' = {45^0} \Rightarrow \angle O'BK = {45^0}\)

\( \Rightarrow \Delta O'A'B\) vuông tại \(O' \Rightarrow O'A' \bot O'B\).

Kéo dài OB’ cắt đường tròn \(\left( O \right)\) tại \(D\). Dễ dàng chứng minh được \(ODB'O\) là hình bình hành \( \Rightarrow OB//O'D \Rightarrow OB//\left( {O'AD} \right)\)

\( \Rightarrow d\left( {OB;O'A} \right) = d\left( {OB;\left( {O'AD} \right)} \right) = d\left( {O;\left( {O'AD} \right)} \right)\) .

Gọi E là trung điểm của AD \( \Rightarrow OE \bot AD\).

Trong \(\left( {OO'E} \right)\) kẻ \(OH \bot O'E\) ta có :

\(\left\{ \begin{array}{l}AD \bot OE\\AD \bot OO'\end{array} \right. \Rightarrow AD \bot \left( {OO'E} \right) \Rightarrow AD \bot OH\)

\(\left\{ \begin{array}{l}OH \bot O'E\\OH \bot AD\end{array} \right. \Rightarrow OH \bot \left( {O'AD} \right) \Rightarrow d\left( {O;\left( {O'AD} \right)} \right) = OE\).

Ta có \(OE\) là đường trung bình của tam giác \(AB'D \Rightarrow OE = \frac{1}{2}AB' = \frac{1}{2}.4\sqrt 2  = 2\sqrt 2 \) (Do tam giác \(OAB'\) vuông cân tại O có \(OA = 4\) nên \(AB' = 4\sqrt 2 \)).

Áp dụng hệ thức lượng trong tam giác vuông OO’E ta có : \(OH = \frac{{OE.OO'}}{{\sqrt {O{E^2} + OO{'^2}} }} = \frac{{2\sqrt 2 .4}}{{\sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {4^2}} }} = \frac{{4\sqrt 3 }}{3}\).

Vậy \(d\left( {O'A;OB} \right) = \frac{{4\sqrt 3 }}{3}\).

Chọn D.