Phương pháp giải:

Đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = g\left( x \right)\) có duy nhất 1 điểm chung \( \Leftrightarrow \) phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right)\) có nghiệm duy nhất.

Lời giải chi tiết:

Phương trình hoành độ giao điểm của đồ thị hai đồ thị hàm số là:

\({x^3} - 3mx + 3 = 3x + 1 \Leftrightarrow {x^3} - 3\left( {m + 1} \right)x + 2 = 0\;\;\;\left( * \right)\)

Hai đồ thị hàm số có duy nhất 1 điểm chung khi và chỉ khi phương trình (*) có nghiệm duy nhất.

\(\left( * \right) \Leftrightarrow {x^3} - 3x + 2 = 3mx\)

Xét \(x = 0 \Leftrightarrow 2 = 0\) (vô lí) \( \Rightarrow x = 0\) không là nghiệm của (*)

\( \Leftrightarrow 3m = \frac{{{x^3} - 3x + 2}}{x} = {x^2} - 3 + \frac{2}{x} = f\left( x \right)\,\,\left( {x \ne 0} \right)\)

\(f'\left( x \right) = 2x - \frac{2}{{{x^2}}} = 0 \Leftrightarrow {x^3} = 1 \Leftrightarrow x = 1\).

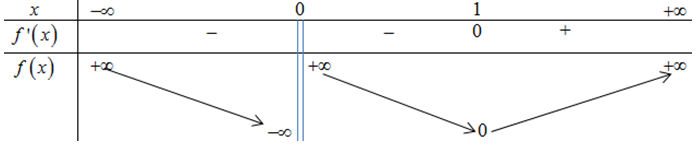
BBT:

Phương trình có nghiệm duy nhất khi và chỉ khi \(3m < 0 \Leftrightarrow m < 0\).

Kết hợp điều kiện đề bài ta ta có: \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left[ { - 2018;0} \right)\end{array} \right. \Rightarrow \) Có 2018 giá trị nguyenr của m thỏa mãn.

Chọn D.