Câu hỏi
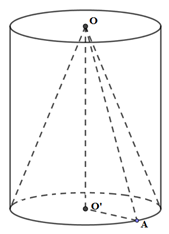
Một hình trụ có hai đáy là hai hình tròn \(\left( {O;r} \right)\) và \(\left( {O';r} \right).\) Khoảng cách giữa hai đáy là \(OO' = r\sqrt 3 .\) Một hình nón có đỉnh là \(O\) và có đáy là hình tròn \(\left( {O';r} \right).\) Gọi \({S_1}\) là diện tích xung quanh của hình trụ và \({S_2}\) là diện tích xung quanh của hình nón. Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}.\)
- A \(\frac{{{S_1}}}{{{S_2}}} = \frac{2}{{\sqrt 3 }}.\)
- B \(\frac{{{S_1}}}{{{S_2}}} = 2\sqrt 3 .\)
- C \(\frac{{{S_1}}}{{{S_2}}} = 2.\)
- D \(\frac{{{S_1}}}{{{S_2}}} = \sqrt 3 .\)
Phương pháp giải:
Diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi rl = 2\pi rh\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\).
Lời giải chi tiết:
Diện tích xung quanh của hình trụ : \({S_1} = 2\pi rh = 2\pi r.r\sqrt 3 = 2\pi \sqrt 3 {r^2}\)
\(\Delta OO'A\) vuông tại O’ \( \Rightarrow OA = \sqrt {OO{'^2} + O'{A^2}} = \sqrt {3{r^2} + {r^2}} = 2r\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl = \pi r.2r = 2\pi {r^2}\)\( \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \sqrt 3 .\)
Chọn D.