Phương pháp giải:

- Đếm số phần tử của không gian mẫu (số cách quân vua di chuyển \(3\) bước).

- Đếm số khả năng có lợi cho biến cố quân vua sau \(3\) bước thì quay về vị trí đầu.

- Tính xác suất.

Lời giải chi tiết:

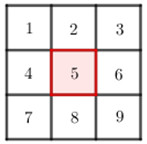
Giả sử quân vua đang ở vị trí số \(5\) (hình vẽ). Ta đếm số các cách quân vua đi ngẫu nhiên \(3\) bước.

Bước 1: có \(8\) cách đi.

Bước 2: có \(8\) cách đi.

Bước 3: có \(8\) cách đi.

Do đó có \({8^3}\) cách quân vua đi ngẫu nhiên \(3\) bước.

Ta đếm số cách quân vua đi \(3\) bước mà quay về đúng vị trí đầu.

TH1: Quân vua đi vào vị trí chéo \(\left( {1,3,7,9} \right)\) ở bước đầu tiên.

Nếu đi vào vị trí số \(1\) thì có \(2\) cách đi thỏa mãn là \(1 - 2 - 5\) và \(1 - 4 - 5\).

Tương tự với các vị trí \(3,7,9\), mỗi cách cũng có \(2\) cách đi thỏa mãn.

Nên có \(4.2 = 8\) cách đi thỏa mãn.

TH2: Quân vua đi vào vị trí kề nó \(\left( {2,4,6,8} \right)\) ở bước đầu tiên.

Nếu đi vào vị trí số \(2\) ở bước đầu thì quân vua có \(4\) cách đi là \(2 - 1 - 5;2 - 3 - 5;2 - 4 - 5;2 - 6 - 5\).

Tương tự với các vị trí \(4,6,8\), mỗi cách cũng có \(4\) cách đi thỏa mãn.

Nên có \(4.4 = 16\) cách đi thỏa mãn trong trường hợp này.

Do đó có tất cả \(8 + 16 = 24\) cách đi mà quân vua sau \(3\) bước trở về được vị trí đầu.

Vậy xác suất cần tính \(P = \dfrac{{24}}{{{8^3}}} = \dfrac{3}{{64}}\).

Chọn C.