Phương pháp giải:

Từ giả thiết ta suy ra được thiết diện là hình chữ nhật.

Xác định khoảng cách từ trục đến thiết diện bằng khoảng cách từ tâm \(O'\) đến thiết diện.

Tính toán các cạnh hình chữ nhật dựa vào định lý Pytago

Tính diện tích hình chữ nhật bằng tích chiều dài với chiều rộng

Lời giải chi tiết:

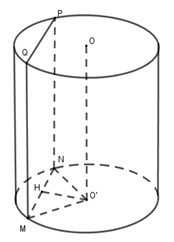
Thiết diện  là hình chữ nhật \(MNPQ\) như hình vẽ.

Kẻ \(O'H \bot MN\) tại \(H\) suy ra \(H\) là trung điểm \(MN\).

 Lại có \(O'H \bot QM\) (do \(QM \bot \) mặt đáy)  nên \(O'H \bot \left( {MNPQ} \right) \Rightarrow O'H = 3\)

Xét tam giác \(O'HN\) vuông tại \(H,\) theo định lý Pytago ta có \(MH = \sqrt {O'{N^2} - O'{H^2}}  = \sqrt {{5^2} - {3^2}}  = \sqrt {16}  = 4\)

Suy ra \(MN = 2MH = 2.4 = 8\)

Hình chữ nhật \(MNPQ\) có \(MQ = OO' = 10;MN = 8 \Rightarrow {S_{MNPQ}} = 10.8 = 80\)

Chọn  C.