Câu hỏi

- A
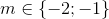
- B m=-2
- C m=-1
- D Không có m
Lời giải chi tiết:
\(\begin{array}{l}y = \frac{1}{3}{x^3} + m{x^2} + \left( {{m^2} + m + 1} \right)x\\ \Rightarrow y' = {x^2} + 2mx + {m^2} + m + 1\\ \Rightarrow y'' = 2x + 2m\end{array}\)
\( \Rightarrow x = 1\) là điểm cực tiểu của hàm số
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}y'\left( 1 \right) = 0\\y''\left( 1 \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}1 + 2m + {m^2} + m + 1 = 0\\2 + 2m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 3m + 2 = 0\\m > - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = - 1\\m = - 2\end{array} \right.\\m > - 1\end{array} \right. \Leftrightarrow m \in \emptyset .\end{array}\)
Chọn D.







