Câu hỏi
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\).
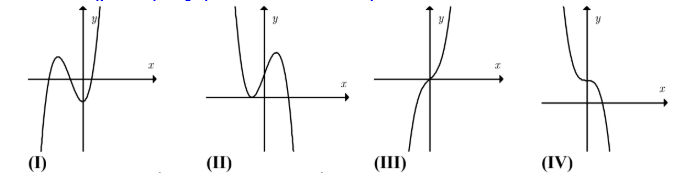
Trong các mệnh đề sau hãy chọn mệnh đề đúng:
- A Đồ thị (III) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) vô nghiệm hoặc có nghiệm kép.
- B Đồ thị (IV) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có nghiệm kép.
- C Đồ thị (II) xảy ra khi \(a \ne 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
- D Đồ thị (I) xảy ra khi \(a < 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
Phương pháp giải:
Sử dụng các dạng đồ thị của hàm số bậc ba xét tính đúng sai của từng đáp án.
Lời giải chi tiết:
Đáp án A: đúng vì dáng đồ thị đi lên từ trái qua phải (hàm đồng biến trên \(\mathbb{R}\)) nên \(a > 0\) và hàm số không có cực trị nên \(f'\left( x \right) = 0\) vô nghiệm hoặc có nghiệm kép.
Đáp án B: sai vì dáng đồ thị đi xuống từ trái qua phải (hàm nghịch biến trên \(\mathbb{R}\)) nên \(a < 0\) chứ không phải \(a > 0\).
Đáp án C: sai vì đồ thị (II) xảy ra khi \(a < 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
Đáp án D: sai vì đồ thị (I) xảy ra khi \(a > 0\) và \(f'\left( x \right) = 0\) có hai nghiệm phân biệt.
Chọn A.







