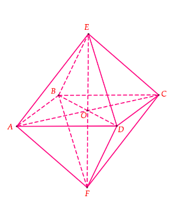
Câu hỏi
Diện tích toàn phần của hình bát diện đều cạnh 3a bằng:
- A \(4{a^2}\sqrt 3 \)
- B \(9{a^2}\sqrt 3 \)
- C \(2{a^2}\sqrt 3 \)
- D \(18{a^2}\sqrt 3 \)
Phương pháp giải:
Khối bát diện đều được ghép từ hai khối chóp tứ giác đều.
Diện tích toàn phần của hình chóp tứ giác đều = Tổng diện tích của 8 mặt bên của khối bát diện = 2 x diện tích xung quan của khối chóp tứ giác đều.
Diện tích xung quanh của hình chóp tứ giác đều = tổng diện tích của các mặt bên của hình chóp tứ giác đều.
Lời giải chi tiết:
Ta có: \({S_{xq\;EABCD}} = 4{S_{EAB}} = 4.\dfrac{{{{\left( {3a} \right)}^2}\sqrt 3 }}{4} = 9{a^2}\sqrt 3 .\)
\( \Rightarrow {S_{EABCDF}} = 2{S_{xq\;EABCD}} = 18{a^2}\sqrt 3 .\)
Chọn D.