Phương pháp giải:

Diện tích mặt cầu có bán kính R là: \({S_{mc}} = 4\pi {R^2}\).

Lời giải chi tiết:

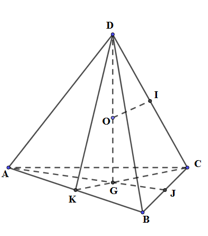
Xét tứ diện đều ABCD có cạnh đều bằng a. Gọi G là tâm tam giác ABC, I, J lần lượt là trung điểm của CD, BC \( \Rightarrow \left\{ \begin{array}{l}DG \bot \left( {ABC} \right)\\CG = \dfrac{2}{3}CK = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\end{array} \right.\)

Dựng mặt trung trực của CD, cắt DG tại O. Khi đó, O là tâm mặt cầu ngoại tiếp tứ diện ABCD.

* Tính R:

Tam giác DGC vuông tại G \( \Rightarrow DG = \sqrt {D{C^2} - G{C^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}}  = \dfrac{{\sqrt 6 a}}{3}\)

\(\Delta DOI\) đồng dạng \(\Delta DCG \Rightarrow \dfrac{{OD}}{{DC}} = \dfrac{{DI}}{{DG}} \Rightarrow \dfrac{{OD}}{a} = \dfrac{{\dfrac{a}{2}}}{{\dfrac{{a\sqrt 6 }}{3}}} \Rightarrow OD = \dfrac{{3a}}{{2\sqrt 6 }} = \dfrac{{a\sqrt 6 }}{4} \Rightarrow R = \dfrac{{a\sqrt 6 }}{4}\)

* Tính diện tích mặt cầu: \({S_{mc}} = 4\pi {R^2} = 4\pi {\left( {\dfrac{{a\sqrt 6 }}{4}} \right)^2} = \dfrac{3}{2}\pi {a^2}\)

Chọn: B