Câu hỏi
Hình chóp SABC có đáy là tam giác vuông tại B, hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Tâm cầu ngoại tiếp hình chóp là:
- A Trung điểm của SB
- B Trung điểm của AC.
- C Trung điểm của SC.
- D Trọng tâm tam giác SAB.
Phương pháp giải:
\(\left\{ \begin{array}{l}\left( \alpha \right) \bot \left( \gamma \right)\\\left( \beta \right) \bot \left( \gamma \right)\\\left( \alpha \right) \cap \left( \beta \right) = d\end{array} \right. \Rightarrow d \bot \left( \gamma \right)\)
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right)\)
Gọi I, F lần lượt là trung điểm của SC, SA, AC
Do tam giác ABC vuông tại B
\( \Rightarrow \) F là tâm đường tròn ngoại tiếp tam giác ABC (1)
IF là đường trung bình của tam giác SAC \( \Rightarrow \)IF // SA
Mà \(SA \bot \left( {ABC} \right) \Rightarrow IF \bot \left( {ABC} \right)\) (2)
Từ (1), (2) suy ra \(IA = IB = IC\)
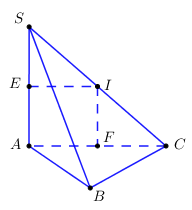
Lại có: tam giác SAC vuông tại A \( \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác SAC
\( \Rightarrow \,IS = IA = IC\)\( \Rightarrow \,IS = IA = IB = IC \Rightarrow I\) là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Chọn: C







