Phương pháp giải:

Hàm số đồng biến trên \(\left( {a;\;b} \right) \Leftrightarrow y' \ge 0\;\;\forall x \in \left( {a;\;b} \right).\)

Lời giải chi tiết:

Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( {3;\;5} \right) \Leftrightarrow y' > 0\;\;\forall x \in \left( {3;\;5} \right)\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 3x + {m^2} + 5m + 6 \ge 0\;\;\forall x \in \left( {3;\;5} \right)\\ \Leftrightarrow {x^2} - 3x \ge  - {m^2} - 5m - 6\;\;\forall x \in \left( {3;\;5} \right)\;\;\;\left( * \right)\end{array}\)

Đặt \(g\left( x \right) = {x^2} - 3x\)

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow g\left( x \right) \ge  - {m^2} - 5m - 6\;\;\forall x \in \left( {3;\;5} \right)\\ \Rightarrow  - {m^2} - 5m - 6 \le \mathop {\min }\limits_{\left( {3;\;5} \right)} g\left( x \right).\end{array}\)

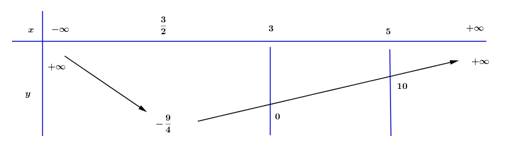
Khảo sát hàm số \(g\left( x \right) = {x^2} - 3x\) ta được:

\( \Rightarrow  - {m^2} - 5m - 6 \le 0 \Leftrightarrow {m^2} + 5m + 6 \ge 0 \Leftrightarrow \left[ \begin{array}{l}m \ge  - 2\\m \le  - 3\end{array} \right.\)

Chọn  B.