Câu hỏi
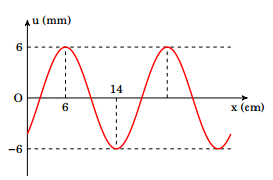
Một sóng cơ lan truyền trên một sợi dây dài nằm ngang, với tốc độ 80 cm/s theo chiều dương trục Ox. Hình dạng của sợi dây tại thời điểm t = 0 được mô tả như hình vẽ. Phương trình sóng truyền trên sợi dây có dạng
- A \(u=6\cos \left( 10\pi t-\frac{\pi x}{8}-\frac{2\pi }{3} \right)\) ; u : mm ; x :cm ; t :s
- B \(u=6\cos \left( 5\pi t-\frac{3\pi }{4} \right)\) ; u : mm ;; t :s
- C \(u=6\cos \left( 10\pi t-\frac{\pi x}{8}+\frac{3\pi }{4} \right)\) ; u : mm ; x :cm ; t :s
- D \(u=6\cos \left( 10\pi t-\frac{\pi x}{8}-\frac{3\pi }{4} \right)\) ; u : mm ; x :cm ; t :s
Phương pháp giải:
Phương trình sóng truyền đi : \(u=A\cos (\omega t+\varphi -\frac{2\pi x}{\lambda })\)
Với A là biên độ sóng, λ là bước sóng, φ là pha ban đầu và ω là tốc độ góc.
Bước sóng λ = v/f
Liên hệ giữa tốc độ góc và tần số: ω = 2πf
Lời giải chi tiết:
Phương trình sóng truyền đi : \(u=A\cos (\omega t+\varphi -\frac{2\pi x}{\lambda })\)
Nhìn vào đồ thị ta thấy u có giá trị lớn nhất là 6mm nên A = 6mm
Khoảng cách giữa cực đại và cực tiểu là 14 – 6 = 8cm nên bước sóng là λ = 16cm
Tần số sóng : f = v/λ = 80/16 = 5Hz Vậy nên ω = 2πf = 10π rad/s
Tại thời điểm t = 0 phần tử sóng đang ở vị trí li độ âm và chuyển động theo chiều dương nên pha ban đầu chỉ có thể là -3π/4 (ứng với góc phần tư thứ 3)
Vậy phương trình sóng thu được là :
\(u=6\cos (10\pi t-\frac{3\pi }{4}-\frac{2\pi x}{16})\)
Với x tính theo cm, t tính theo giây, u tính theo mm.