Câu hỏi
Cho hàm số có bảng biến thiên:
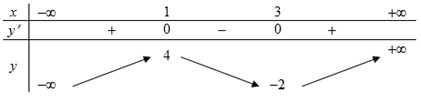
Tìm tất cả các giá trị của \(m\) để bất phương trình \(f\left( {\sqrt {x - 1} + 1} \right) \le m\) có nghiệm?
- A \(m \ge 1\).
- B \(m \ge - 2\).
- C \(m \ge 4\).
- D \(m \ge 0\).
Phương pháp giải:
+) Đặt \(t\left( x \right) = \sqrt {x - 1} + 1 \ge 1\), đưa bất phương trình về dạng \(f\left( t \right) \le m\). Phương trình có nghiệm khi và chỉ khi \(\mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( t \right) \le m\).
+) Dựa vào BBT, nhận xét và kết luận.
Lời giải chi tiết:
Đặt \(t\left( x \right) = \sqrt {x - 1} + 1 \ge 1\) khi đó ta có \(f\left( t \right) \le m\) (*)
Để phương trình (*) có nghiệm \(t \ge 1\) thì \(\mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( t \right) \le m\).
Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( t \right) = - 2 \Rightarrow m \ge - 2\).
Chọn B.







