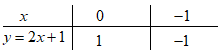Phương pháp giải:

Thay tọa độ điểm \(M\left( { - 1; - 1} \right)\) vào công thức hàm số \(\left( 1 \right)\) để tìm m.

+) Với giá trị m vừa tìm được, ta thay vào công thức hàm số và vẽ đồ thị hàm số trên mặt phẳng tọa độ.

Lời giải chi tiết:

Đồ thị hàm số \(\left( 1 \right)\) đi qua điểm \(M\left( { - 1; - 1} \right)\) nên ta có:

\( - 1 = m\left( { - 1} \right) + 1 \Leftrightarrow m = 2\;\;\left( {tm} \right)\)

Vậy với \(m = 2\) thì đồ thị hàm số đã cho đi qua điểm \(M\left( { - 1; - 1} \right).\)

Với \(m = 2\) ta có: \(y = 2x + 1.\)

Ta có bảng giá trị:

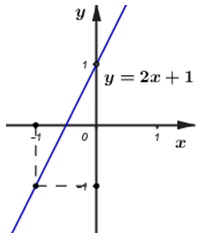
Vậy đồ thị hàm số \(y = 2x + 1\) là đường thẳng đi qua hai điểm \(\left( {0;\;1} \right),\;\left( { - 1; - 1} \right).\)

Chọn B.

Phương pháp giải:

Hai đường thẳng \({d_1}:\;\;y = {a_1}x + {b_1}\) và \({d_2}:\;y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)

Lời giải chi tiết:

Điều kiện \(m \ne 0.\)

Đường thẳng \(y = mx + 1\;\;\left( 1 \right)\) song song với đường thẳng \(\left( d \right):\;y = \left( {{m^2} - 2} \right)x + 2m + 3\)

\( \Leftrightarrow \left\{ \begin{array}{l}m = {m^2} - 2\\2m + 3 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - m - 2 = 0\\2m \ne  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m =  - 1\\m = 2\end{array} \right.\\m \ne  - 1\end{array} \right. \Leftrightarrow m = 2\;\;\left( {tm} \right)\)

Vậy \(m = 2\) thỏa mãn điều kiện bài toán.

Chọn C.

Phương pháp giải:

Gọi H  là hình chiếu của O trên đường thẳng \(\left( 1 \right).\) Khi đó áp dụng hệ thức lượng trong tam giác vuông để tính độ dài OH.

Lời giải chi tiết:

Điều kiện \(m \ne 0.\)

Gọi \(A,\;B\) lần lượt là các giao điểm của đường thẳng \(\left( 1 \right)\) với các trục \(Ox,\;Oy.\)

Khi đó ta có: \(A\left( {{x_1};\;0} \right),\;\;B\left( {0;\;{y_2}} \right).\)

\( \Rightarrow \left\{ \begin{array}{l}0 = m{x_1} + 1\\m.0 + 1 = {y_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} =  - \frac{1}{m}\\{y_2} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A\left( { - \frac{1}{m};\;0} \right)\\B\left( {0;\;1} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}OA = \left| { - \frac{1}{m}} \right| = \frac{1}{{\left| m \right|}}\\OB = \left| 1 \right| = 1\end{array} \right..\)

Gọi \(H\) là hình chiếu của \(O\) trên đường thẳng \(\left( 1 \right) \Rightarrow OH = \frac{2}{{\sqrt 5 }}.\)

Khi đó ta có \(\Delta AOB\) vuông tại \(O\) và có đường cao \(OH.\)

Áp dụng hệ thức lượng cho \(\Delta AOB\) vuông tại \(O\) và có đường cao \(OH\)  ta có:

\(\begin{array}{l}\;\;\;\;\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{2}{{\sqrt 5 }}} \right)}^2}}} = \frac{1}{{{{\left| {{x_1}} \right|}^2}}} + \frac{1}{{{{\left| {{y_2}} \right|}^2}}}\\ \Leftrightarrow \frac{5}{4} = \frac{1}{{{{\left( { - \frac{1}{m}} \right)}^2}}} + \frac{1}{{{1^2}}} \Leftrightarrow \frac{5}{4} = {m^2} + 1\\ \Leftrightarrow 5 = 4{m^2} + 4 \Leftrightarrow 4{m^2} = 1 \Leftrightarrow {m^2} = \frac{1}{4} \Leftrightarrow m =  \pm \frac{1}{2}\;\left( {tm} \right)\end{array}\)

Vậy \(m =  \pm \frac{1}{2}\) thỏa mãn điều kiện bài toán.

Chọn C.