Phương pháp giải:

1) Thay \(m = 2\) vào phương trình đường thẳng \(\left( d \right)\) sau đó lập bảng giá trị và vẽ đồ thị hàm số.

2) Đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a'x + b' \Leftrightarrow \left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\)

3) Tìm giao điểm của \(y = x + 3\) với các trục Ox, Oy, sau đó sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Lời giải chi tiết:

Cho hàm số \(y = \left( {m - 1} \right)x + 3\)  có đồ thị là đường thẳng (d)

1) Vẽ đường thẳng (d) khi \(m = 2\)

Khi \(m = 2\) thì (d): \(y = x + 3\)

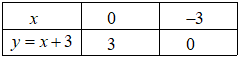
Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( d \right)\;\;y = x + 3\) là đường thẳng  đi qua 2 điểm \(\left( {0;3} \right),\left( { - 3;0} \right)\) 

2) Tìm m để đường thẳng (d) song song với đường thẳng \(y = 2x + 1\)

Để đường thẳng (d) song song với đường thẳng \(y = 2x + 1\)

\( \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 2\\3 \ne 1\end{array} \right. \Leftrightarrow m = 3\)

Vậy với \(m = 3\) thỏa mãn yêu cầu đề bài.

3) Tính khoảng cách từ gốc tọa độ đến đường thẳng được vẽ ở câu 1

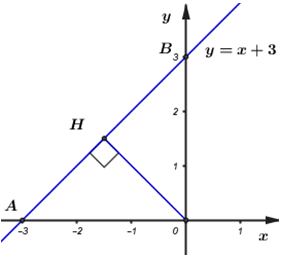
Gọi A, B lần lượt là giao điểm của đường thẳng \(y = x + 3\) với hai trục Ox, Oy

\( \Rightarrow A\left( { - 3;0} \right),\,\,\,B\left( {0;3} \right) \Rightarrow OA = OB = 3\)

Gọi H là hình chiếu của O trên AB. (như hình vẽ)

Áp dụng hệ thức lượng trong tam giác OAB vuông cân tại O, đường cao OH ta có:

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} = \frac{1}{9} + \frac{1}{9} = \frac{2}{9} \Rightarrow O{H^2} = \frac{9}{2} \Rightarrow OH = \frac{{3\sqrt 2 }}{2}\;\;\;\left( {OH > 0} \right).\)  

Vậy khoảng cách từ gốc tọa độ đến \(\left( d \right):\;y = x + 3\) là \(OH = \frac{{3\sqrt 2 }}{2}.\)

Chọn A.