Phương pháp giải:

Lập BBT của đồ thị hàm số \(y = 3{x^4} + 8{x^3} - 6{x^2} - 24x – m\), từ đó suy ra BBT của đồ thị hàm số \(y = \left| {3{x^4} + 8{x^3} - 6{x^2} - 24x - m} \right|\) trong trường hợp có 7 điểm cực trị.

Lời giải chi tiết:

Xét hàm số \(y = 3{x^4} + 8{x^3} - 6{x^2} - 24x – m\) ta có \(y' = 12{x^3} + 24{x^2} - 12x - 24 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\\x =  - 2\end{array} \right.\).

BBT:

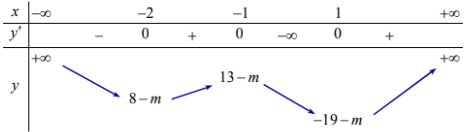
Dựa vào BBT ta thấy để đồ thị hàm số \(y = \left| {3{x^4} + 8{x^3} - 6{x^2} - 24x - m} \right|\) có 7 điểm cực trị \( \Leftrightarrow \left\{ \begin{array}{l}8 - m < 0\\13 - m > 0\end{array} \right. \Leftrightarrow 8 < m < 13 \Rightarrow m \in \left\{ {9;10;11;12} \right\} \Rightarrow \sum m  = 42\).

Chọn D.