Câu hỏi
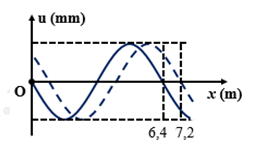
Cho một sợi dây cao su căng ngang. Làm cho đầu O của dây dao động theo phương thẳng đứng. Hình vẽ mô tả hình dạng sợi dây tại thời điểm t1 (đường nét liền) và t2= t1 + 0,2s (đường nét đứt). Tại thời điểm t3 = t2 + 0,4s thì độ lớn li độ của phần tử M cách đầu dây một đoạn 2,4m (tính theo phương truyền sóng) là \(\sqrt 3 cm\). Gọi δ là tỉ số của tốc độ cực đại của phần tử trên dây với tốc độ truyền sóng. Giá trị của δ gần giá trị nào nhất sau đây?
- A 0,025.
- B 0,022.
- C 0,012.
- D 0,018.
Phương pháp giải:
Sử dụng lí thuyết về sự truyền sóng, vòng tròn lượng giác và kĩ năng đọc đồ thị.
Lời giải chi tiết:
Từ đồ thị ta có: \(\lambda =6,4m\)
Vận tốc truyền sóng : \(v=\frac{\Delta {{x}_{12}}}{\Delta {{t}_{12}}}=\frac{7,2-6,4}{0,2}=4m/s\)
Tần số góc dao động của các phần tử :
\(\omega =\frac{2\pi }{T}=\frac{2\pi }{\frac{\lambda }{v}}=\frac{2\pi .v}{\lambda }=\frac{2\pi .4}{6,4}=\frac{5\pi }{4}rad/s\)
Độ lệch pha giữa M và O:
\(\begin{gathered}
\Delta \varphi = \Delta {\varphi _x} + \Delta {\varphi _t} = \frac{{2\pi .\Delta {x_{13}}}}{\lambda } + \omega .\Delta {t_{13}} \hfill \\
\,\,\,\,\,\,\,\,\, = \frac{{2\pi .2,4}}{{6,4}} + \frac{{5\pi }}{4}\left( {0,2 + 0,4} \right) = \frac{{3\pi }}{2}rad \hfill \\
\end{gathered} \)
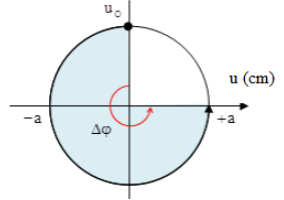
Biểu diễn trên VTLG:
Từ VTLG ta có:
\({{u}_{M}}=a=\sqrt{3}cm\Rightarrow \delta =\frac{\omega A}{v}=\frac{\frac{5\pi }{4}.\sqrt{3}{{.10}^{-2}}}{4}=0,017\)
Chọn D.