Câu hỏi
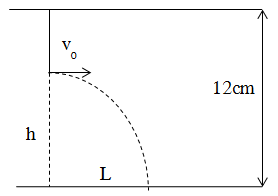
Một con lắc đơn có chiều dài l được treo dưới gầm cầu cách mặt nước 12 m. Con lắc đơn dao động điều hòa với biên độ góc α0 = 0,1 rad. Khi vật đi qua vị tri cân bằng thì dây bị đứt. Khoảng cách cực đại ( tính theo phương ngang) từ điểm treo con lắc đến điểm mà vật nặng rơi trên mặt nước mà con lắc thể đạt được là.
- A 75 cm.
- B 95 cm.
- C 65 cm.
- D 85 cm.
Phương pháp giải:
Sử dụng lí thuyết về dao động điều hòa của con lắc đơn kết hợp với chuyển động ném ngang
Lời giải chi tiết:
Gọi khoảng cách từ VTCB của con lắc đến mặt nước là h
=> dây treo con lắc có chiều dài l = 12 – h
Vận tốc của con lắc khi đi qua VTCB: \({v_0} = {v_{\max }} = \sqrt {gl\alpha _0^2} = \sqrt {g(12 - h)\alpha _0^2} \)
Tại đây, dây treo con lắc bị đứt => con lắc sẽ chuyển động như một vật bị ném ngang với vận tốc ban đầu v0
=> Tầm bay xa : \(L = {v_0}\sqrt {\frac{{2h}}{g}} = \sqrt {2(12 - h)h\alpha _0^2} = {\alpha _0}\sqrt 2 .\sqrt {(12 - h).h} \)
Nhận xét: \(\sqrt {(12 - h).h} \le \frac{{12 - h + h}}{2} = 6\)(theo Cô-si) =>\(L \le 6\sqrt 2 {\alpha _0} \approx 0,85m = 85cm\)
Vậy Lmax = 85cm => Chọn D