Câu hỏi
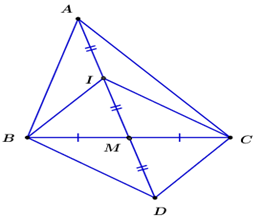
Cho ABC có AM là trung tuyến. Gọi I là trung điểm AM. Chọn mệnh đề đúng:
- A \(\overrightarrow {IB} + \overrightarrow {IC} + 2\overrightarrow {IA} = \vec 0\)
- B \(2\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} = \vec 0\)
- C \(\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {IA} = \vec 0\)
- D \(\overrightarrow {IB} + 2\overrightarrow {IC} + 3\overrightarrow {IA} = \vec 0\)
Phương pháp giải:
Sử dụng hệ thức trung điểm đoạn thẳng và quy tắc hình bình hành để tìm mối qua hệ giữa \(\overrightarrow {IA} ,\,\,\overrightarrow {IB} ,\,\,\overrightarrow {IC} \)
Lời giải chi tiết:
Gọi D là điểm đối xứng với I qua M
\( \Rightarrow \) IBDC là hình bình hành (2 đường chéo cắt nhau tại trung điểm của mỗi đường)
Theo quy tắc hình bình hành ta được \(\overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow {ID} = 2\overrightarrow {IM} \)
Mặt khác có I là trung điểm của AM \( \Rightarrow \overrightarrow {IM} = - \overrightarrow {IA} \)
\( \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} = - 2\overrightarrow {IA} \Rightarrow \overrightarrow {IB} + \overrightarrow {IC} + 2\overrightarrow {IA} = \overrightarrow 0 \)
Chọn A.