Câu hỏi
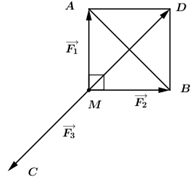
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M. Tìm cường độ lực \(\overrightarrow {{F_3}} \)
- A 86,60 N
- B 100 N
- C 70,71 N
- D 70,17 N
Phương pháp giải:
Áp dụng quy tắc hình bình hành.
Vật đứng yên khi tổng các lực tác động lên điểm bằng 0.
Lời giải chi tiết:
Có cường độ lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) đều bằng 50 N và tam giác MAB vuông tại M
\( \Rightarrow \) Tam giác MAB vuông cân tại M
Lấy điểm D sao cho MADB là hình vuông
\( \Rightarrow MD = \sqrt {M{A^2} + A{D^2}} = \sqrt {M{A^2} + M{B^2}} = 50\sqrt 2 \,\,N\)
Vì vật đứng yên nên tổng các lực tác động lên điểm bằng 0
\( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {{F_3}} = - \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) = - \overrightarrow {MD} \)
Vậy lực \(\overrightarrow {{F_3}} \) có hướng ngược với \(\overrightarrow {MD} \) và có cường độ bằng \(50\sqrt 2 \,\,N \approx 70,71\,\,N\)
Chọn C.