Câu hỏi
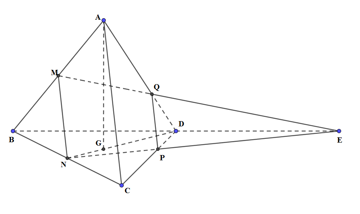
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V . Tính V .
- A \(V = \dfrac{{\sqrt 2 {a^3}}}{{18}}\)
- B \(V = \dfrac{{11\sqrt 2 {a^3}}}{{216}}\)
- C \(V = \dfrac{{13\sqrt 2 {a^3}}}{{216}}\)
- D \(V = \dfrac{{7\sqrt 2 {a^3}}}{{216}}\)
Phương pháp giải:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó, \(\dfrac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\)
Lời giải chi tiết:
Gọi P, Q lần lượt là giao điểm của NE và CD; của ME và AD. Khi đó, thiết diện của khối tứ diện cắt bởi mặt phẳng (MNE) là tứ giác MNPQ.
*) Tính thể tích khối tứ diện đều ABCD:
Tam giác BCD đều, có các cạnh đều bằng a
\( \Rightarrow {S_{BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
G là trọng tâm tam giác BCD
\( \Rightarrow GD = \dfrac{2}{3}ND = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
Tam giác AGD vuông tại G \( \Rightarrow AG = \sqrt {A{D^2} - G{D^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt 6 }}{3}\)
Thể tích khối tứ diện đều ABCD là: \(V = \dfrac{1}{3}.AG.{S_{BCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Dễ dàng chứng minh Q, P lần lượt là trọng tâm các tam giác ABE, BCE \( \Rightarrow \dfrac{{QE}}{{ME}} = \dfrac{{PE}}{{NE}} = \dfrac{2}{3}\)
Ta có: \(\dfrac{{{V_{E.DQP}}}}{{{V_{E.BMN}}}} = \dfrac{{EQ}}{{EM}}.\dfrac{{EP}}{{EN}}.\dfrac{{ED}}{{EB}} = \dfrac{2}{3}.\dfrac{2}{3}.\dfrac{1}{2} = \dfrac{2}{9}\) \( \Rightarrow {V_{BMN.DQP}} = \dfrac{7}{9}{V_{E.BMN}}\)
*) Tính thể tích khối chóp E.BMN:
\({V_{E.BMN}} = \dfrac{1}{3}.d\left( {M,\left( {BCD} \right)} \right).{S_{\Delta BNE}} = \dfrac{1}{3}.\dfrac{1}{2}d\left( {A,\left( {BCD} \right)} \right).{S_{\Delta BCD}}\) \( = \dfrac{1}{2}{V_{ABCD}}\) (do \({S_{BNE}} = 2{S_{BND}} = 2.\dfrac{1}{2}{S_{BCD}} = {S_{BCD}}\))
\( \Rightarrow {V_{BMN.DQP}} = \dfrac{7}{9}{V_{E.BMN}} = \dfrac{7}{9}.\dfrac{1}{2}{V_{ABCD}} = \dfrac{7}{{18}}{V_{ABCD}}\)
Gọi V là thể tích khối đa diện chứa đỉnh A \( \Rightarrow V = {V_{ABCD}} - {V_{BMN.DQP}} = \dfrac{{11}}{{18}}{V_{ABCD}} = \dfrac{{11}}{{18}}.\dfrac{{{a^3}\sqrt 2 }}{{12}} = \) \(\dfrac{{11\sqrt 2 {a^3}}}{{216}}\).
Chọn: B