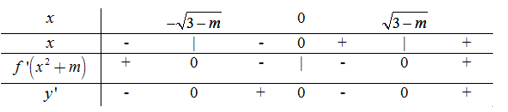Câu hỏi
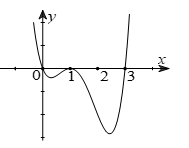
Cho hàm số \(y = f(x)\). Hàm số \(y = f'(x)\)có đồ thị như hình vẽ dưới đây.
Có bao nhiêu giá tri nguyên của \(m\) để hàm số \(y = f({x^2} + m)\) có \(3\) điểm cực trị.
- A 3
- B 4
- C 2
- D 1
Phương pháp giải:
+) Sử dụng công thức tính đạo hàm hàm hợp để tính y’.
+) Giải phương trình \(y' = 0\).
Lời giải chi tiết:
Ta có: \(y = f\left( {{x^2} + m} \right) \Rightarrow y' = 2x.f'\left( {{x^2} + m} \right)\)
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} + m} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} + m = 0\\{x^2} + m = 3\end{array} \right.\) (do tại \(x = 1\) ta có\(y = f'(x)\) không đổi dấu) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - m\\{x^2} = 3 - m\end{array} \right.\)
+) \(m = 0\) ta có \(y' = 0 \Rightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 3 \end{array} \right.\)
\(y' = 0\) tại 3 điểm \(x = 0,\,\,x = \sqrt 3 ,\,\,x = - \sqrt 3 \) và đổi dấu tại 3 điểm này \( \Rightarrow m = 0\) thỏa mãn
+) \(m = 3\) ta có \(y' = 0 \Leftrightarrow x = 0\)\( \Rightarrow m = 3\) không thỏa mãn
+) \(m < 0\)
\(y' = 0\) có 5 nghiệm phân biệt \(x = 0,\,x = \pm \sqrt { - m} ,\,\,\,x = \pm \sqrt {3 - m} \)
Hàm số có 5 cực trị \( \Rightarrow \) Loại các giá trị \(m < 0\).
+) \(m > 3\)
Phương trình \(y' = 0\) có 1 nghiệm duy nhất \(x = 0\) và đổi dấu tại 1 điểm duy nhất \(x = 0\) \( \Rightarrow \) Loại các giá trị \(m > 3\)
+) \(0 < m < 3\)
\(y' = 0\) có 3 nghiệm phân biệt \(x = 0,\,\,\,x = \pm \sqrt {3 - m} \)
Hàm số có 3 cực trị \(x = 0,\,\,\,x = \pm \sqrt {3 - m} \)\( \Rightarrow \) Các giá trị \(0 < m < 3\) thỏa mãn
Mà \(m \in Z \Rightarrow m \in \left\{ {1;2} \right\}\)
Kết luận: Để hàm số \(y = f({x^2} + m)\) có \(3\) điểm cực trị thì \(m \in \left\{ {0;1;2} \right\}\): có 3 giá trị m thỏa mãn.
Chọn: A