Câu hỏi
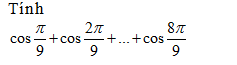
- A 0
- B 1
- C 2
- D 3
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\cos \alpha = - \cos \left( {\pi - \alpha } \right)\\ \Rightarrow \cos \dfrac{\pi }{9} = - \cos \left( {\pi - \dfrac{\pi }{9}} \right) = - \cos \left( {\dfrac{{8\pi }}{9}} \right)\\ \Rightarrow \cos \dfrac{\pi }{9} + \cos \dfrac{{8\pi }}{9} = 0\end{array}\)
\(\begin{array}{l} \Rightarrow \cos \dfrac{\pi }{9} + \cos \dfrac{{2\pi }}{9} + ... + \cos \dfrac{{8\pi }}{9}\\ = \left( {\cos \dfrac{\pi }{9} + \cos \dfrac{{8\pi }}{9}} \right) + \left( {\cos \dfrac{{2\pi }}{9} + \cos \dfrac{{7\pi }}{9}} \right) + \left( {\cos \dfrac{{3\pi }}{9} + \cos \dfrac{{6\pi }}{9}} \right) + \left( {\cos \dfrac{{4\pi }}{9} + \cos \dfrac{{5\pi }}{9}} \right)\\ = 0 + 0 + 0 + 0 = 0\end{array}\)
Chọn A







