Câu hỏi
Sóng dừng trên dây có tần số f = 20Hz và truyền đi với tốc độ 1,6 m/s. Bụng sóng dao động với biên độ 3cm. Gọi N là vị trí của một nút sóng, C và D là hai vị trí cân bằng của hai phần tử trên dây cách N lần lượt là 9cm và 32/3cm và ở 2 bên của N. Tại thời điểm t1 li độ của phần tử tại điểm C là \( - \sqrt 2 cm\) và đang hướng về VTCB. Vào thời điểm t2 = t1 + 9/40s li độ của phần tử tại điểm D là
- A
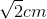
- B
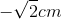
- C
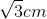
- D
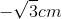
Phương pháp giải:
Sử dụng lí thuyết về sóng dừng
Lời giải chi tiết:
λ = v/f = 8 cm
* Ta có CN =9 cm= λ + λ /8 ; ND = 32/3 cm = λ + λ /3
+ C cách 1 nút là λ /8 => biên độ dao động tại C là : \({A_C} = {\rm{ }}2a|sin{{2\pi d} \over \lambda }| = {\rm{ }}2a\left| {sin{{2\pi {\lambda \over 8}} \over \lambda }} \right| = {\rm{ a}}\sqrt 2 \)
+ D cách 1 nút là λ/3 => biên độ dao động tại D là :\({A_D} = {\rm{ }}2a|sin{{2\pi d} \over \lambda }| = {\rm{ }}2a\left| {sin{{2\pi {\lambda \over 3}} \over \lambda }} \right| = {\rm{ a}}\sqrt 3 \)
* Các phần tử trên cùng 1 bó sóng luôn dao động cùng pha, 2 bó sóng cạnh nhau luôn dao động ngược pha. Từ hình vẽ suy ra uC và uD dao động ngược pha. Ta có
\({u_C} = a\sqrt 2 \cos \omega t;{u_D} = - a\sqrt 3 \cos \omega t \Rightarrow {{{u_C}} \over {{u_D}}} = - {{\sqrt 2 } \over {\sqrt 3 }} \Rightarrow {u_D} = - {u_C}{{\sqrt 3 } \over {\sqrt 2 }}\)
* Ta có Δt = t2 – t1 = 9/40 s = 2T + T/2
Ở thời điểm t1 : \({u_C} = - \sqrt 2 cm\) => ở thời điểm t2 : \({u_C} = \sqrt 2 cm\)
=> Ở thời điểm t2 : \({u_D} = {u_C}{{ - \sqrt 3 } \over {\sqrt 2 }} = - \sqrt 3 cm\)
Chọn D







