Câu hỏi
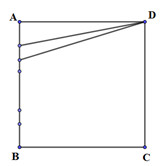
Cho hình vuông ABCD. Trên cạnh AB lấy n điểm khác nhau, không trùng với A, B. Biết có 16 tam giác được tạo thành từ n + 4 điểm (A, B, C, D và n điểm nói trên). Giá trị của n bằng:
- A 5
- B 3
- C 2
- D 4
Phương pháp giải:
+) Tính số tam giác được tạo thành.
+) Tìm n.
Lời giải chi tiết:
Số tam giác lập từ n + 4 điểm bất kì là: \(C_{n + 4}^3\)
Số bộ 3 điểm trong n + 2 điểm phân biệt, thẳng hàng là: \(C_{n + 2}^3\)
Số tam giác được tạo thành từ n + 4 điểm (A, B, C, D và n điểm nói trên) là: \(C_{n + 4}^3 - C_{n + 2}^3\)
Theo đề bài, ta có:
\(\begin{array}{l}C_{n + 4}^3 - C_{n + 2}^3 = 16 \Leftrightarrow \dfrac{{\left( {n + 4} \right)!}}{{\left( {n + 1} \right)!3!}} - \dfrac{{\left( {n + 2} \right)!}}{{\left( {n - 1} \right)!3!}} = 16\\ \Leftrightarrow \dfrac{{\left( {n + 4} \right)\left( {n + 3} \right)\left( {n + 2} \right)}}{6} - \dfrac{{\left( {n + 2} \right)\left( {n + 1} \right)n}}{6} = 16\\ \Leftrightarrow \left( {n + 4} \right)\left( {n + 3} \right)\left( {n + 2} \right) - \left( {n + 2} \right)\left( {n + 1} \right)n = 96\\ \Leftrightarrow \left( {n + 2} \right)\left( {\left( {n + 4} \right)\left( {n + 3} \right) - \left( {n + 1} \right)n} \right) = 96 \Leftrightarrow \left( {n + 2} \right)\left( {6n + 12} \right) = 96\\ \Leftrightarrow {\left( {n + 2} \right)^2} = 16 \Leftrightarrow n + 2 = 4 \Leftrightarrow n = 2\end{array}\)
Chọn: C







