Câu hỏi
Trong các khối trụ có cùng diện tích toàn phần bằng \(\pi \), gọi \((\gamma )\) là khối trụ có thể tích lớn nhất, chiều cao của\((\gamma )\) bằng:
- A \(\dfrac{\pi }{3}\).
- B \(\dfrac{{\sqrt 6 }}{3}\).
- C \(\dfrac{{\sqrt 6 }}{6}\).
- D \(\dfrac{{\pi \sqrt 3 }}{4}\).
Phương pháp giải:
Xét hàm số, tìm GTLN.
Lời giải chi tiết:
Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ.
Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = \pi \Rightarrow h = \dfrac{{1 - 2{R^2}}}{{2R}}\)
Do \(h > 0 \Rightarrow 1 - 2{R^2} > 0 \Leftrightarrow {R^2} < \dfrac{1}{2} \Leftrightarrow 0 < R < \dfrac{{\sqrt 2 }}{2}\).
Thể tích khối trụ: \(V = \pi {R^2}h = \pi {R^2}.\dfrac{{1 - 2{R^2}}}{{2R}} = \dfrac{{\pi \left( {R - 2{R^3}} \right)}}{2}\)
Xét hàm số \(g\left( R \right) = \dfrac{\pi }{2}\left( {R - 2{R^3}} \right)\) trên \(\left( {0;\dfrac{{\sqrt 2 }}{2}} \right)\).
Ta có: \(g'\left( R \right) = \dfrac{\pi }{2}\left( {1 - 6{R^2}} \right),\,\,g'\left( R \right) = 0 \Leftrightarrow R = \dfrac{{\sqrt 6 }}{6}\,\,\left( {Do\,\,R > 0} \right)\)
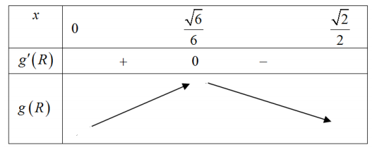
Bảng biến thiên:
Vậy, thể tích khối trụ lớn nhất khi \(R = \dfrac{{\sqrt 6 }}{6} \Rightarrow h = \dfrac{{\sqrt 6 }}{3}\).
Chọn: B