Câu hỏi
Tàu ngầm đang ở trên mặt biển bỗng đột ngột lặn xuống theo phương tạo với mặt nước biển một góc \({21^o}\). Nếu tàu chuyển động theo phương lặn xuống được 300m thì nó ở độ sâu bao nhiêu? Khi đó khoảng cách theo phương nằm ngang so với nơi xuất phát là bao nhiêu mét ? (kết quả làm tròn đến mét)
- A Tàu lặn xuống độ sâu 104 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 260 (m)
- B Tàu lặn xuống độ sâu 109 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 270 (m)
- C Tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m)
- D Tàu lặn xuống độ sâu 119 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 290 (m)
Phương pháp giải:
Áp dụng các công thức sin và cosin để tính các đại lượng đề bài yêu cầu
Lời giải chi tiết:
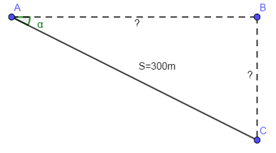
Coi mặt biển là một mặt phẳng, theo đề bài ta có hình vẽ minh họa:
Trong hình vẽ ta có:
+) Đoạn AC là quãng đường tàu di chuyển trong quá trình lặn,
+) Đoạn BC là độ sâu mà tàu lặn được.
+) Đoạn AB là khoảng cách theo phương ngang tính từ vị trí xuất phát tới vị trí của tàu sau khi lặn.
+) \(\alpha \) là góc tạo bởi quãng đường tàu chuyển động và mặt biển.
Xét tam giác vuông ABC vuông tại B có:
+) \(\sin \alpha = \frac{{BC}}{{AC}} \Rightarrow BC = AC.\sin \alpha = 300.\sin {21^o} \approx 107\left( m \right)\)
+) \(\cos \alpha = \frac{{AB}}{{AC}} \Rightarrow AB = AC.\cos \alpha = 300.cos{21^o} = 280\left( m \right)\)
Vậy tàu lặn xuống độ sâu 107 (m) và khoảng cách theo phương ngang từ vị trí ban đầu tới vị trí sau khi lặn là 280 (m).
Chọn C.