Câu hỏi
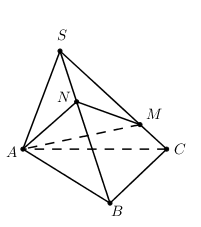
Cho hình chóp S.ABC có thể tích \(V = 8\). M, N là hai điểm sao cho \(\overrightarrow {SM} = 3\overrightarrow {MC} ;\,\,\overrightarrow {SB} = 3\overrightarrow {SN} \) và diện tích tam giác AMN bằng 2. Tính khoảng cách từ S đến mặt phẳng (AMN).
- A \(d = \frac{9}{2}\)
- B \(d = 1\)
- C \(d = \frac{3}{2}\)
- D \(d = 3\)
Phương pháp giải:
\(d\left( {S;\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{AMN}}}}\)
Lời giải chi tiết:
Ta có : \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ACB}}}} = \dfrac{{SM}}{{SC}}.\dfrac{{SN}}{{SB}} = \dfrac{3}{4}.\dfrac{1}{3} = \dfrac{1}{4} \Rightarrow {V_{S.AMN}} = \dfrac{1}{4}{V_{S.ABC}} = 2\)
\( \Rightarrow d\left( {S;\left( {AMN} \right)} \right) = \frac{{3{V_{S.AMN}}}}{{{S_{AMN}}}} = \dfrac{3.2}{2} = 3\).
Chọn D.
Câu hỏi trước
