Câu hỏi
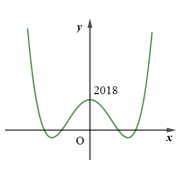
Hàm số \(y = {x^4} - 2017{x^2} + 2018\) có giá trị cực đại là
- A \({{y}_{C}}=\sqrt{2017}\).
- B \({{y}_{C}}=0\).
- C \({{y}_{C}}=\sqrt{2018}\).
- D \({{y}_{C}}=2018\).
Lời giải chi tiết:
\(y = {x^4} - 2017{x^2} + 2018 \Rightarrow y' = 4{x^3} - 4034x,\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt {\frac{{2017}}{2}} \end{array} \right.\)
Hàm số đạt cực đại tại \(x=0,\,\,{{y}_{C}}=2018\).
Chọn: D
Câu hỏi trước
