Phương pháp giải:

- Tách \(3n + 5 = 3n + 3 + 2 = 3\left( {n + 1} \right) + 2.\)

Khi đó \((3n + 5):(n + 1) = 3 + \frac{2}{{n + 1}}\).

Để \(3n + 5\)  chia hết cho \(n + 1\)  thì 2 phải chia hết cho \(n + 1\), suy ra \(n + 1 \in U\left( 2 \right),\)  từ đó ta tìm được \(n.\)

Lời giải chi tiết:

Ta có : \(3n + 5 = 3n + 3 + 2 = 3\left( {n + 1} \right) + 2.\)

Khi đó ta có: \((3n + 5):(n + 1) = \frac{{3.(n + 1)}}{{n + 1}} + \frac{2}{{n + 1}} = 3 + \frac{2}{{n + 1}}\).

Để \(3n + 5\)  chia hết cho \(n + 1\)  thì 2 phải chia hết cho \(n + 1\), suy ra \(n + 1 \in U\left( 2 \right).\) 

Lại có: \(U\left( 2 \right) = \left\{ { - 2; - 1;\;1;\;2} \right\}.\)

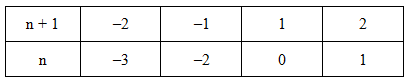
Ta có bảng sau:

Vì  n là số tự nhiên nên \(n \in {\rm{\{ 0;}}\,\,1{\rm{\} }}\).
Vậy để \(3n + 5\) chia hết cho \(n + 1\) thì \(n \in {\rm{\{ 0}}\,{\rm{;}}\,\,{\rm{1\} }}\).

Chọn B.