Câu hỏi
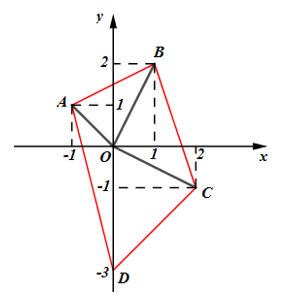
Trong mặt phẳng phức, gọi A, B, C, D lần lượt là các điểm biểu diễn các số phức \({z_1} = - 1 + i,\) \(\,\,{z_2} = 1 + 2i,\,\,{z_3} = 2 - i,\,\,{z_4} = - 3i\). Gọi S diện tích tứ giác ABCD. Tính S.
- A \(S = \frac{{17}}{2}\)
- B \(S = \frac{{19}}{2}\)
- C \(S = \frac{{23}}{2}\)
- D \(S = \frac{{21}}{2}\)
Phương pháp giải:
+) Tính diện tích các tam giác OAB, OBC, OCD, OAD.
+) Sử dụng công thức \({S_{\Delta OAB}} = \frac{1}{2}d\left( {O;AB} \right).AB\)
Lời giải chi tiết:
Ta có: \(A\left( { - 1;1} \right);\,\,B\left( {1;2} \right);\,\,C\left( {2; - 1} \right);\,\,D\left( {0; - 3} \right)\).
Phương trình AB: \(\frac{{x + 1}}{{1 + 1}} = \frac{{y - 1}}{{2 - 1}} \Leftrightarrow x + 1 = 2y - 2 \Leftrightarrow x - 2y + 3 = 0 \Rightarrow d\left( {O;AB} \right) = \frac{3}{{\sqrt 5 }};\,\,AB = \sqrt 5 \)
\( \Rightarrow {S_{\Delta OAB}} = \frac{1}{2}d\left( {O;AB} \right).AB = \frac{1}{2}.\frac{3}{{\sqrt 5 }}.\sqrt 5 = \frac{3}{2}\)
Phương trình BC: \(\frac{{x - 1}}{{2 - 1}} = \frac{{y - 2}}{{ - 1 - 2}} \Leftrightarrow - 3x + 3 = y - 2 \Leftrightarrow 3x + y - 5 = 0 \Rightarrow d\left( {O;BC} \right) = \frac{5}{{\sqrt {10} }};\,\,BC = \sqrt {10} \)
\( \Rightarrow {S_{\Delta OBC}} = \frac{1}{2}d\left( {O;BC} \right).BC = \frac{1}{2}.\frac{5}{{\sqrt {10} .\sqrt {10} }} = \frac{5}{2}\)
Phương trình CD: \(\frac{{x - 2}}{{0 - 2}} = \frac{{y + 1}}{{ - 3 + 1}} \Leftrightarrow - 2x + 4 = - 2y - 2 \Leftrightarrow x - y - 3 = 0 \Rightarrow d\left( {O;CD} \right) = \frac{3}{{\sqrt 2 }};\,\,CD = 2\sqrt 2 \)
\( \Rightarrow {S_{\Delta OCD}} = \frac{1}{2}.\frac{3}{{\sqrt 2 }}.2\sqrt 2 = 3\)
Phương trình AD: \(\frac{{x + 1}}{{0 + 1}} = \frac{{y - 1}}{{ - 3 - 1}} \Leftrightarrow - 4x - 4 = y - 1 \Leftrightarrow 4x + y + 3 = 0 \Rightarrow d\left( {O;AD} \right) = \frac{3}{{\sqrt {17} }};\,\,AD = \sqrt {17} \)
\( \Rightarrow {S_{\Delta OAD}} = \frac{1}{2}.\frac{3}{{\sqrt {17} }}.\sqrt {17} = \frac{3}{2}\)
Vậy \(S = {S_{\Delta OAB}} + {S_{\Delta OBC}} + {S_{\Delta OCD}} + {S_{\Delta OAD}} = \frac{{17}}{2}\).
Chọn đáp án A.