Câu hỏi
Trên dây đàn hồi đang có sóng dừng ổn định với khoảng cách giữa hai vị trí cân bằng giữa nút và bụng cạnh nhau là 6cm. Tốc độ truyền sóng trên dây 1,2 m/s, biên độ dao động tại bụng là 4cm. Gọi N là một nút. P, Q là hai điểm trên dây có vị trí cân bằng cách N lần lượt là 15cm và 16cm và ở hai bên của N. Tại thời điểm t, P có li độ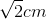 
và đang hướng về vị trí cân bằng . Sau đó một khoảng thời gian ngắn nhất ∆t thì Q có li độ 3cm và đang hướng về vị trí biên. Tìm ∆t.
- A 7/6s
- B 1/6s
- C 1/20s
- D 7/120s
Phương pháp giải:
- Sử dụng đường tròn lượng giác
- Sử dụng lí thuyết về khoảng cách giữa 1 bụng và 1 nút liên tiếp trong sóng dừng
- Sử dụng công thức tính biên độ dao động của một điểm trên sóng dừng
Lời giải chi tiết:
Bụng và nút cách nhau 1/4 bước sóng nên bước sóng λ/4 = 6 => λ = 24 cm
T = λ/v = 0,2 s
\({A_P} = 2.2.\left| {\sin \left( {2\pi {{15} \over {24}}} \right)} \right| = 2\sqrt 2 cm\)
\({A_Q} = 2.2.\left| {\sin \left( {2\pi {{16} \over {24}}} \right)} \right| = 2\sqrt 3 cm\)
Hai phần tử P và Q ngược pha nhau: \({{{u_P}} \over {{u_Q}}} = - {{{A_P}} \over {{A_Q}}} = - {{\sqrt 2 } \over {\sqrt 3 }}\)
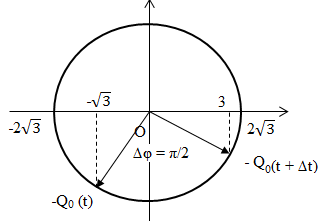
Tại thời điểm t: P có li độ \(\sqrt 2 cm\) và đang hướng về vị trí cân bằng thì \({u_Q} = - \sqrt 3 cm\) và đang đi lên ứng với Q0(t) trên đường tròn. Sau khoảng thời gian ngắn nhất ∆t thì Q có li độ bằng 3cm và hướng về vị trí biên. Biểu diễn trên đường tròn lượng giác ta được:
Từ đường tròn lượng giác ta tính được góc quét ∆φ = π/2 (rad) => ∆t = T/4 = 0,2/4 = 1/20 (s)
Câu hỏi trước
